19 September 2022 | Draft
Cognitive Embodiment of Patterns of Governance of Higher Order
Memorable navigation of viable global pathways from 4-fold to 64-fold and beyond
-- / --
Introduction
Cognitive analogues of mechanical transmission systems?
Fundamental pattern of order in space-time
Configurations of polyhedra as transmission systems
Alternative configurations of polyhedral transmission systems
Vertical arrays of polyhedra implying higher degrees of order
Nested and cage-like polyhedral configurations implying degrees of implicate order
Implicate order through hypercube and drilled truncated cube?
Polyhedral representation of Sustainable Development Goals including "Own Goals"?
Toroidal polyhedral ring arrays
Dynamics of systemic connectivity as a challenge to invariance
Strategic implications of traditional angelic and demonic configurations?
Traditionally intuited system diagrams for governance?
Distinguishing requisite variety: requisite dependence on "other" perspectives
Variable geometry of institutions as alternation between comprehensible polyhedral patterns
References
Produced, coincidentally, on the occasion of the 7th World Congress on the Square of Opposition (Leuven, September 2022)
Introduction
Little needs to be said of the chaotic state of global governance and the crises with which it is faced at this time. It therefore continues to be useful to question the methods advocated and deployed to address the challenges as they are currently framed. It is necessarily perceived as presumptuous to assert the merit of alternatives, however vigorously their merits are described. The arguments against any alternatives are themselves vigorously articulated -- with little ability to transcend the dysfunctional consequences of this dynamic.
The challenges of the times are curiously exemplified by a strangely unquestioned relation to numbers (Comprehension of Numbers Challenging Global Civilization, 2014). History may see it as bizarre that a global civilization should be so preoccupied with 1.5 -- being, however coincidentally, both the key to the response to the pandemic through social distancing, and as the target cap on global warming (Humanity's Magic Number as 1.5? Dimensionless constant governing civilization and its potential collapse, 2020). Claire Lemercieris and Claire Zalc ask whether history is a matter of individual agency and action, or of finding and quantifying underpinning structures and patterns (History by Numbers, Aeon/Psyche, 2 September 2022). That argument cites the curious historical focus of economists on the productivity engendered in slave populations in the USA by an average of 0.7 whippings per hand per year.
With respect to assumptions of the vital need for economic growth, a limited set of statistics are a preoccupation for governance, including interest rates, inflation rates, tax rates, exchange rates -- and rates of growth, as indicated by GDP. The tendency is an invitation to satire, given the neglect of other indicators -- especially in the light of the current proxy war with Russia (Evaluating the Grossness of Gross Domestic Product: Refugees Per Kiloton (RPK) as a missing indicator? 2016). As illustrated by past military activity in the Afghanistan arena, the focus is indeed on performance with little attention to remedial capacity (Remedial Capacity Indicators versus Performance Indicators, 1981; Transforming the Unsustainable Cost of General Education: strategic insights from Afghanistan, 2009). There is general resignation to the extraordinary level of national debt of many leading countries, and its continuing increase -- a "black hole" of astronomical proportions.
Many global statistical reports are indeed produced offering insight into performance, but with little insight into remedial capacity over time (Dynamic Transformation of Static Reporting of Global Processes , 2013). The foreseeable consequences of increasing population growth are assiduously avoided -- incommunicable as a fundamentally inconvenient truth (Institutionalized Shunning of Overpopulation Challenge, 2008). Curiously there is a strange global dependence on obscure metrics of proven fallibility (Uncritical Strategic Dependence on Little-known Metrics: the Gaussian Copula, the Kaya Identity, and what else? 2009).
Potentially even more curious for the future is what might otherwise be framed as simple superstition, namely an unquestioned global preference for strategies articulated by particular numbers: 7, 8, 10, 14, 20 or 30, exemplified by the 12-fold (Checklist of 12-fold Principles, Plans, Symbols and Concepts, 2011). There is no systemic explanation for the 17-fold articulation of the Sustainable Development Goals of the United Nations (Systemic Coherence of the UN's 17 SDGs as a Global Dream, 2021).
In this context there is therefore a case for continuing to speculate on distinctive ways of ordering information about the current global condition. The aim in what follows is to elicit imaginative responses from a perspective which contrasts with the conventional articulation of proposals in bullet-pointed text. The weakness of such articulations is evident from the lack of relationship between the points made in any such checklist -- undermining any systemic implications and relevance. That pattern of connectivity is of a very low order. This ensures that the memorability of such a checklist is itself of a very low order and is effectively a guarantee that any acclaimed institutional "oversight" is associated with "blindspots" -- as ironically implied by the alternative understanding of "oversight".
For example, who is able to recall all 17 of the UN's Sustainable Development Goals (let alone its 169 tasks)? Who has any sense of the manner in which they interact with each other together to ensure their systemic viability? Is this equally true of the rights articulated in the UN's Universal Declaration of Human Rights?
In a world in which great emphasis is placed on the attractiveness and interest of visual representations and music -- with which people are indeed happy to engage -- why is so much reliance placed on text in the processes of governance? This occurs in a period in which governance is increasingly experienced as alienating, opaque, and untrustworthy -- and only too evidently incompetent. The contrast with engagement with song is remarkable, as has been appreciated by some autocrats (A Singable Earth Charter, EU Constitution or Global Ethic? 2006).
What follows is a speculative quest for distinctive patterns of order which have a possibility of eliciting imaginative responses -- at least for some. It follows from a case previously made (Time for Provocative Mnemonic Aids to Systemic Connectivity? 2018). The challenge is especially evident in the case of the problematic articulation of the core values of a civilization aspiring to democracy -- and faced with its obvious inadequacies (Values, Virtues and Sins of a Viable Democratic Civilization, 2022). The focus is on the related patterns of numbers which are widely upheld as of fundamental significance to the organization of memory, especially computer memory, following their earlier consideration (Cognitive organization by polyhedra of 16, 32 and 64 vertices, 2017; Polyhedral Pattern Language, 2008)
The approach explored is notably inspired by the visual representation by Keith Critchlow (Order in Space: a design source book, 1969). This offered a coherent visual insight into the closest packing of the 13 disparate, semi-regular Archimedean polyhedral forms -- in contrast with the 5 more familiar Platonic forms recognized for their spherical regularity, and widely valued for symbolic purposes. Critchlow later adapted this geometrical insight into the organization of flowers (The Hidden Geometry of Flowers: living rhythms form and number, 2011). Such insights focus the question of the "closest packing" of disparate information essential to its memorability.
The Archimedean forms have acquired particular significance in oppositional logic, namely the discipline which focuses on the organization of logical relations as they feature in discourse and in computerized search algorithms. Unfortunately the coherent representation of these logical operations with polyhedra has as yet translated only to the most limited degree into relevance to the challenges of governance, as indicated separately (Oppositional Logic as Comprehensible Key to Sustainable Democracy, 2018). Ironically, opposition to wider application of those insights has not evoked any form of self-reflective inquiry by that discipline.
The exploration in what follows is a quest for the unusual and the extraordinary in the configuration of information. It is not envisaged as a specific explanation or proposal but rather as a challenge to the imagination -- to the possibility and sense of "what if". It can be argued that we unconsciously inhabit what amounts to "cognitive glass houses". The question is the degree to which these are usefully recognized as "conceptual cages" within which we are effectively "incarcerated" -- whether as greenhouses or with glass ceilings. The edges of polyhedra are usefully suggestive of the bars of such cages, irrespective of their more valuable connotations.
If there is a need for "cages" of previously unimagined design -- as might well be easily enabled for intelligent primates in zoos (Primate Environmental Enrichment: automated reconfiguration of zoo enclosures, 2011). Changing metaphor, the argument is illustrated by the widespread familiarity with gear change mechanisms on bicycles and in automobile transmission systems. Under what circumstances do we need to "change gear" conceptually -- and how many gears might be appropriate to experience a higher degree of freedom? This frames the question of the need for conceptual "cage changing mechanisms" in 3D and 4D -- and their possibility in practice.
Symbolically it might be asked what relationship this might bear to Jacob's ladder as a linear inspiration for the Abrahamic religions. This suggests the possibility of a non-linear "cognitive ladder", as with the inspiration offered by the coiling of DNA, namely the pattern so fundamental to biological life (Climbing Elven Stairways: DNA as a macroscopic metaphor of polarized psychodynamics, 2007). To the extent that it is widely appreciated that the house of divinity "has many mansions", this invites recognition of the possibility that it also has many "stairwells". The dynamic can be explored as the quest for alternative and more integrative paradigms (Navigating Alternative Conceptual Realities, 2002; Combining Clues to 'Ascent' and 'Escape', 2002).
The argument concludes with a presentation of the relationship between the hypercube (of significance to oppositional logic) and the 64-edged drilled truncated cube. The role of this polyhedron can be understood as a form of Rosetta Stone offering a means of reconciling a range of patterns variously upheld as of strategic significance: 4-fold, 6-fold, 7-fold, 8-fold, 9-fold, 12-fold, 14-fold, 16-fold, 20-fold, 32-fold and 64-fold. The argument is extended to a 72-fold pattern of traditional significance.
For a civilization faced with an unprecedented global migration crisis, this migration process could be understood as disguising the degree to which there is effectively a mass migration of humanity to a new cognitive frontier -- meriting a degree of recognition, as separately argued (Future Global Exodus to the Metasphere, 2022).
Cognitive analogues of mechanical transmission systems?
Inspiration is increasingly sought for technological innovation through the insights offered by biomimicry and biomimetics -- most obviously with respect to airplane design and flight. Inspiration can be similarly found for cognitive innovation from both biomimicry and technomimicry (Technomimicry as Analogous to Biomimicry, 2011), as illustrated from the process of helicopter development (Engendering a Psychopter through Biomimicry and Technomimicry, 2011). Potentially of greater relevance to governance are the insights to be drawn from the work of Nikola Tesla, most notably with respect to the alternation and rotation of magnetic fields (Reimagining Tesla's Creativity through Technomimicry, 2014).
There is widespread familiarity with the transmission systems vital to the operation of automobiles and bicyles. The process of changing gear -- and the need to do so -- calls for little commentary with regard to movement over terrain presenting different challenges. Far less evident is the cognitive equivalent requiring a shift from one mode of organization to another in response to "cognitive terrain" of different degrees of complexity.
Whilst familiar, the process of changing gear in an automobile is less evident in terms of the mechanical geometry of the invisible transmission system (or "gear box"). This can be surprisingly complex in the case of heavy duty trucks (see gift shift pattern, below left).
By contrast, the mechanism in the case of bicycles is especially visible (see below). As expressed by Wikipedia:
Bicycle gearing is the aspect of a bicycle drivetrain that determines the relation between the cadence, the rate at which the rider pedals, and the rate at which the drive wheel turns. On some bicycles there is only one gear and, therefore, the gear ratio is fixed, but most modern bicycles have multiple gears and thus multiple gear ratios. A shifting mechanism allows selection of the appropriate gear ratio for efficiency or comfort under the prevailing circumstances: for example, it may be comfortable to use a high gear when cycling downhill, a medium gear when cycling on a flat road, and a low gear when cycling uphill. Different gear ratios and gear ranges are appropriate for different people and styles of cycling....
On single-speed bicycles and multi-speed bicycles using derailleur gears, the gear ratio depends on the ratio of the number of teeth on the crankset to the number of teeth on the rear sprocket (cogset).... On a bicycle, the cassette or cluster is the set of multiple sprockets that attaches to the hub on the rear wheel. A cogset works with a rear derailleur to provide multiple gear ratios to the rider.
| Mechanical metaphors indicative of the nature and possibility of conceptual gear shifting | ||
| As suggested by a gear shift pattern in trucks | A Shimano XT rear derailleur on a mountain bike | 10-speed bicycle cassette |
 |
 |
 |
| C. Corleis, CC BY-SA 3.0, via Wikimedia Commons | Sam Sailor, CC BY-SA 4.0, via Wikimedia Commons | |
Skilled cyclists and car drivers have little difficulty in appreciating that there is an art to changing gear -- and choosing into which gear to shift according to circumstances. As a metaphor, the ability to "change gear" is recognized in rhetoric and in the deployment of complementary strategies. Far less evident is the number of gears between which a choice can be made -- and how and when to "shift gear". Some consideration of the opportunity is evident in discussion of variable institutional geometry (see below).
The configuration of transmission systems merits a degree of comparison with the tradition of basket weaving and its symbolism (The Future of Comprehension: conceptual birdcages and functional basket-weaving, 1980). Ironically the relevance of such a metaphor could be seen in reference to "basket" with respect to the major Conference on Security and Cooperation in Europe as a key element of the détente process during the Cold War. This was organized into three "baskets" of issues (Findings Eleven Years After Helsinki -- Implementation of the Final Act: Basket I, 1987; Basket II, 1987; Basket III, 1987). Use of that insightful metaphor did not however extend to the manner in which the baskets were "woven". It is such relationships which are integral to insight into systemic viability (Interweaving Thematic Threads and Learning Pathways , 2010; E. Ronner, et al, Basket of Options: unpacking the concept, 7 July 2021).
Fundamental pattern of order in space-time
Framed by the potential of technomicry, the question is how to derive cognitive insights from understandings of order in space.
As noted above, the inspiration for the exploration below derives from the early work of Keith Critchlow presented in conventional text form with a static two-dimensional image (below left). This has invited adaptation of that representation into the dynamic three-dimensional visualization enabled by web technology (discussed further below). Critchlow's initiative has inspired other extensions (Robert C. Meurant, A New Order in Space: aspects of a threefold ordering of the fundamental symmetries of empirical space, as evidence in the Platonic and Archimedean polyhedra, International Journal of Space Structures, 6, 1991, 1)
Transformational "route maps"? The relation between the articulations of insights suggestively mapped onto polyhedra offers the further sense that a "cognitive toolkit" could well vary in scope -- in the number of "tools" held to be relevant to a particular set of circumstances. This is suggested by a kind of "route map", discussed separately and reproduced below right (Pathway "route maps" of potential psychosocial transformation? 2015). As indicated there, this might be understood as Polyhedral meta-patterns of relationships? (2015).
| Alternative schematic relationships between 12 Archimedean polyhedra | ||
| Closest packing configuration of polyhedra by Critchlow (enhanced with arrow animation indicating transformations) |
Conway relational chart Showing 12 polyhedral forms created by 3 symmetry-preserving operations on the cube |
Distinctive relationships pathways between spherically symmetrical polyhedra |
|
 |
 |
| Engaging with Globality through Dynamic Complexity, 2009 | Tomruen at English Wikipedia, Public domain, via Wikimedia Commons | F=faces, E=edges, V=vertices (total of these in parenthesis) |
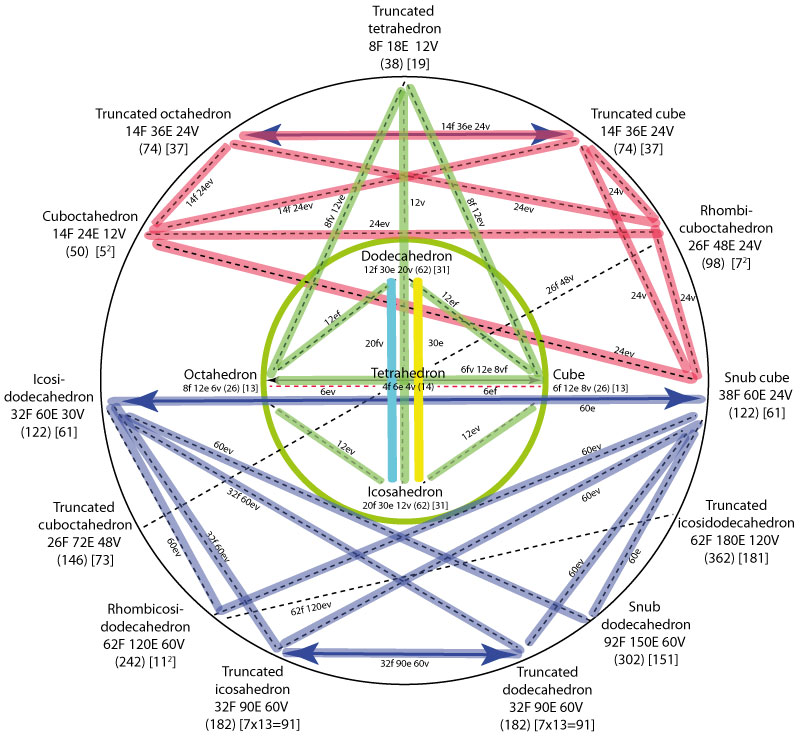
The emphasis of Critchlow's representation is on the geometry of the closest packing of 12 spheres -- clearly with implications for the packaging industry. Given that the semi-regular Archimedean polyhedra are recognized for a degree of spherical symmetry, Critchlow was also able to indicate how 12 of those forms could be arrayed together in a manner respectful of their geometrical relationship.
Critchlow's 12-fold geometrical array of disparate forms around a 13th, calls for recognition of the systemic connectivity implied by the geometry of that configuration, partially suggested by an animation of the connections in his original map (above, left). This can be explored in terms of the geometrical attributes which suggest ways -- pathways -- in which one geometrical form can be transformed into another. This is suggested by the two-dimensional map on the right above.
Method of loci and memorability of the succinct: Curiously "closest packing" invites recognition in terms of mnemonics and memorabilty, as suggested above. It could be argued that the art of memory lies in techniques whereby an array of disparate elements are held together. The principle has been extensively described as the traditional method of loci (Frances Yates, The Art of Memory, 1966). How are disparate elements "packed" compactly into memory -- enabling their succinct expression? As presented in what follows, the features of polyhedra offer "loci" with which "memories" can be variously associated.
Obvious examples include names of relatives and friends, celebrities, events, and songs. Geography poses a challenge with respect to towns, countries, rivers, mountains, and seas. Biology frames the challenge in terms of animal and plant species. Astronomy presents the challenge in terms of planets, stars and galaxies. The geographic example clarifies a further issue, namely how to get from one place to another through s network of roadways. The challenge of remembering relationships is variously evident in the other cases.
A question that would seem to be avoided is the manner in which people remember the details within the domains with which they are especially preoccupied. Are significant proportions of the population effectively "list averse", namely challenged to remember details which take list form? What alternatives do they cultivate in preference to lists -- most notably in traditional oral cultures? How indeed do they organize and remember the relationships between relatives, celebrities, and the like?
Does any significant coherence of the complexities of civilization correspond in any way to the so-called islands of stability discovered by nuclear physicists among the vast array of isotopes of chemical elements?
Symmetry-preserving operations: Of potential relevance to development of this theme is the formal study of transformations between polyhedral forms, as succinctly indicated in the central image above regarding the Conway polyhedron notation, and discussed separately (Topological operations on polyhedra as indicative of cognitive operations, 2021).. This is understood as constrained by symmetry preservation, as separately discussed in considering the encoding of coherent topic transformation in global dialogue (2021):
- Cognitive implications of operational modification of polyhedra -- "global tiling"
- Dialogue coherence through formalization of local symmetry-preserving operations
- Operations transforming polyhedra as modelling transformations of dialogue coherence
- Rendering a 64-fold pattern dynamically comprehensible via 20-fold and 12-fold patterns
"Ways of looking"? The current strategic challenge could be framed otherwise by asking how many "ways of looking" are potentially relevant to creative recognition of any remedial response. The phrase has achieved salience through the inspiration offered by the poem of Wallace Stevens (Thirteen Ways of Looking at a Blackbird, 1917) and the resulting application in a variety of arenas -- beyond authoritative closure on the one right way, as in the case of the pandemic (Variety of "ways of looking" -- binary or otherwise, 2021).
The further challenge is how to interrelate such contrasting perspectives (Interrelating Multiple Ways of Looking at a Crisis, 2021). One approach is through configurations of axes of bias, as discussed separately with respect to values and virtues (Systems of Categories Distinguishing Cultural Biases , 1993; Global ethical nexus of disparate challenges, 2022).
Configurations of polyhedra as transmission systems
Cognitive engines and gear boxes? Technology has been able to develop beyond the 2-stroke engine -- without disregarding its role under particular circumstances. Is it possible to consider more complex "engines" for the democratic process? What insights might be inspired by development of four-stroke engines, six-stroke engines, or even an eight-stroke engine (cf How does an 8-stroke IC engine work? Quora)?
The question framed in what follows is the nature of the "gearbox" which would enable transition between 3-fold, 4-fold, and N-fold modalities, as previously framed (In quest of a "cognitive gearbox" or transmission system, 2021). The complexities of the associated transmission mechanics can be contrasted with simplistic assumptions regarding the communication "transmission" between governors and governed.
Mapping options? There is considerable familiarity with use of simple geometrical forms to map relationships. Most obvious is use of a sphere to map the features of the planet. Less obvious is the extensive array of distinctive projections whereby this may be achieved -- if the map is to be reproduced in two-dimensions (List of Map Projections, Wikipedia). Some of these take the form of polyhedra which can be unfolded from 3D to 2D, as with the so-called Dymaxion Map.
Yet to be a focus of attention is the manner in which information, conventionally ordered by checklists, can be mapped onto polyhedra -- specifically in order to emphasize the systemic relationship between the elements of the checklist. A polyhedron is appropriately understood to be a system in its own right, as asserted by Buckminster Fuller asserted that: All systems are polyhedra: All polyhedra are systems. ((Synergetics: explorations in the geometry of thinking, 1975/1979, 400.56). However, despite the cognitive emphasis implied by the title,the relevance to strategic "thinking" is less than evident, as discussed separately (Geometry of Thinking for Sustainable Global Governance: cognitive implication of synergetics, 2009).
Judicious association of disparate elements on a polyhedral map therefore enables recognition of their systemic integrity. The form of the polyhedron, especially its symmetry, is then a valuable trigger for both the comprehension and memorability significantly absent from articulation in list form (Identifying Polyhedra Enabling memorable Strategic Mapping, 2020). With respect to visualization f organization and strategic coherence through 3D modelling, the latter discusses:
Relative simplicity of strategic articulations: As might be expected, many of the conventional articulations of strategic initiatives are potentially associated with more mappable (and memorable) polyhedra, as indicated in the following table
Cognitive implications: The cognitive implications and strategic relevance of such patterns invite variously explorations:
- The Future of Comprehension: conceptual birdcages and functional basket-weaving, 1980
- Optimizing Web Surfing Pathways for the Overloaded: polyhedral insights from the travelling salesman problem of operations research, 2015
- Embodying Global Hegemony through a Sustaining Pattern of Discourse: cognitive challenge of dominion over all one surveys, 2015
- Dynamics of N-fold Integration of Disparate Cognitive Modalities, 2021
Alternative configurations of polyhedral transmission systems
The following configurations are presented as a trigger for imaginative speculation as being indicative of the predilection for hierarchical modes of organization. In contrast to the use by Keith Critchlow (above) of the truncated tetrahedron as a form of "keystone", here use is made of the simple tetrahedron. The numerical characteristics of each configuration and its elements is appended in each case -- as an indication of mapping possibilities. In each case a progression from 4 (vertices) to 64 is indicated.
| Configuration A | Configuration B | ||
| Non-transparent faces | Transparent faces | Non-transparent faces | Transparent faces |
 |
 |
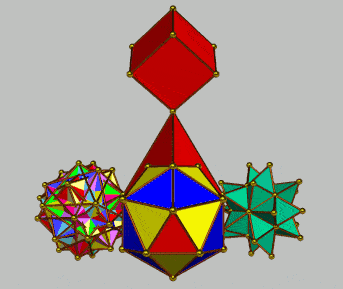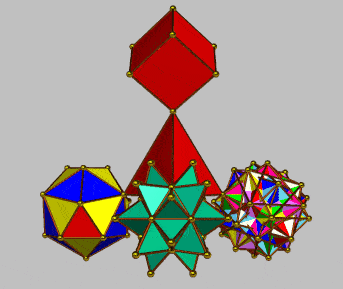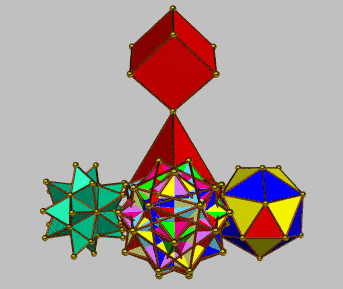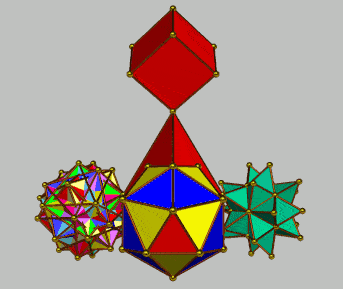 |
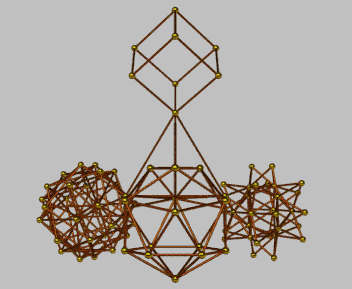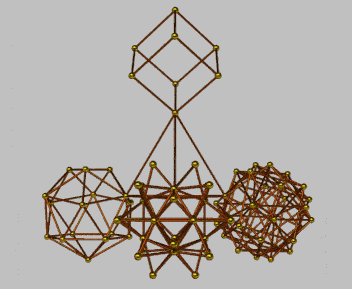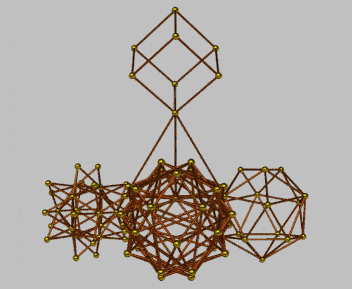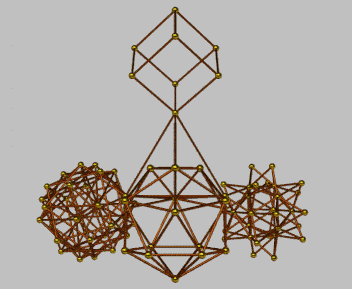 |
| Component polyhedra | Elements (vertices, edges, faces) | Component polyhedra | Elements (vertices, edges, faces) | ||||||||||||
| V | E | F | EV | EF | VF | EVF | V | E | F | EV | EF | VF | EVF | ||
| tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 | tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 |
| cube | 8 | 12 | 6 | 20 | 18 | 14 | 26 | cube | 8 | 12 | 6 | 20 | 18 | 14 | 26 |
| simplest torus | 16 | 28 | 12 | 44 | 40 | 28 | 56 | 1 freq truncated tetrahedron | 16 | 42 | 28 | 58 | 70 | 44 | 86 |
| drilled truncated cube | 32 | 64 | 32 | 96 | 96 | 64 | 128 | augmented icosahedron | 32 | 90 | 60 | 122 | 150 | 92 | 182 |
| 42-Rit proj | 64 | 96 | 64 | 160 | 160 | 128 | 224 | cubes-8 | 64 | 96 | 48 | 160 | 144 | 112 | 208 |
Use is made above of the so-called simplest torus as being of potential interest in ordering the Sustainable Development Goals of the UN (Current relevance of the "simplest torus"? 2019; Coherent mapping possibilities on the simplest torus? 2019).
| Configuration C | Configuration D | ||
| Non-transparent faces | Transparent faces | Non-transparent faces | Transparent faces |
 |
 |
 |
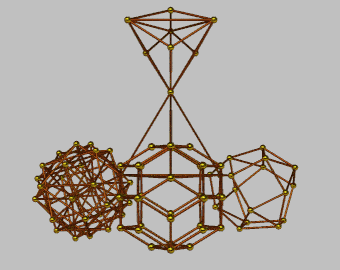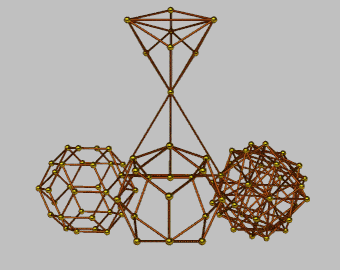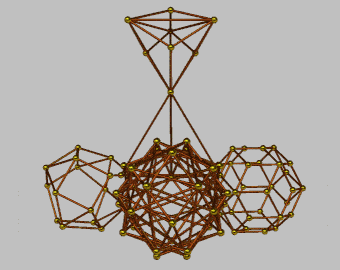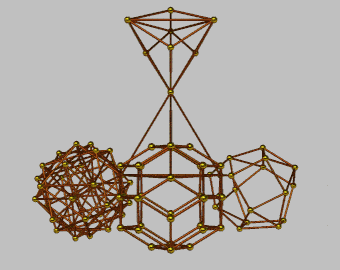 |
| Component polyhedra | Elements (vertices, edges, faces) | Component polyhedra | Elements (vertices, edges, faces) | ||||||||||||
| V | E | F | EV | EF | VF | EVF | V | E | F | EV | EF | VF | EVF | ||
| tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 | tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 |
| triakistetrahedron | 8 | 18 | 12 | 26 | 30 | 20 | 38 | triakistetrahedron | 8 | 18 | 12 | 26 | 30 | 20 | 38 |
| 5-5-4 acrohedron | 16 | 30 | 16 | 46 | 46 | 32 | 62 | 5-5-4 acrohedron | 16 | 30 | 16 | 46 | 46 | 32 | 62 |
| rhombic triacontahedron | 32 | 60 | 30 | 92 | 92 | 122 | 182 | rhombic triacontahedron | 32 | 60 | 30 | 92 | 92 | 122 | 182 |
| 19-Tat proj | 64 | 112 | 48 | 176 | 160 | 112 | 224 | cubes-8 | 64 | 96 | 48 | 160 | 144 | 112 | 208 |
In the animations below, the rotations are no longer made around a "vertical" axis of the tetrahedron.
| Configuration E | Configuration F | ||
| Non-transparent faces | Transparent faces | Non-transparent faces | Transparent faces |
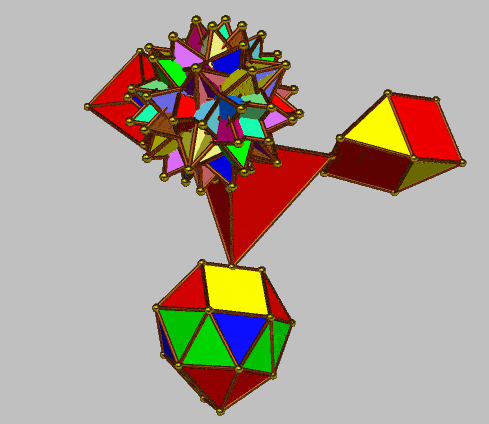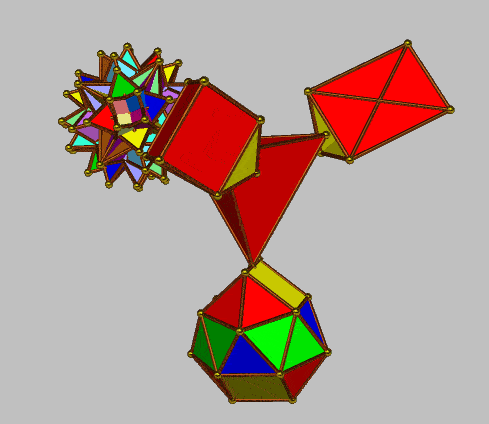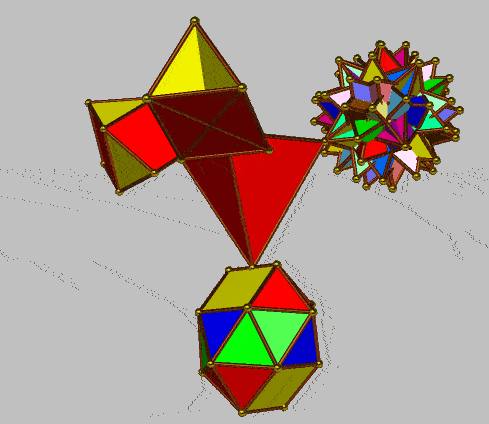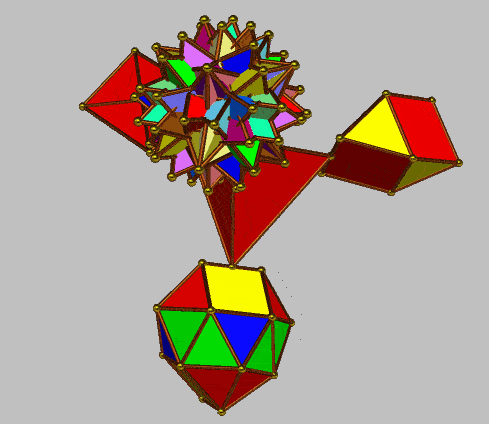 |
 |
 |
 |
| Component polyhedra | Elements (vertices, edges, faces) | Component polyhedra | Elements (vertices, edges, faces) | ||||||||||||
| V | E | F | EV | EF | VF | EVF | V | E | F | EV | EF | VF | EVF | ||
| tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 | tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 |
| gyrobifastigium | 8 | 14 | 8 | 22 | 22 | 16 | 30 | 17-Thor (3) | 8 | 24 | 32 | 32 | 56 | 40 | 64 |
| diphenocingulum | 16 | 38 | 24 | 54 | 62 | 40 | 78 | diphenocingulum | 16 | 38 | 24 | 54 | 62 | 40 | 78 |
| 44-Hinnit | 32 | 96 | 120 | 128 | 216 | 152 | 158 | augmented icosahedron | 32 | 90 | 60 | 122 | 150 | 92 | 182 |
| tetrahedra 8+6+2 | 64 | 96 | 64 | 160 | 160 | 256 | 352 | 19-Tat proj | 64 | 112 | 48 | 176 | 160 | 112 | 224 |
Vertical arrays of polyhedra implying higher degrees of order
There is no lack of references implying the possibility of "higher" degrees of insight -- whether or not the metaphor is to be challenged. The recognition is obvious in the sequence of academic degrees and qualifications, and related assumptions of IQ. It features in secret societies, as with the degrees of Freemasonry; it is a characteristic of initiations and the associated rituals (Varieties of Rebirth: distinguishing ways of being born again, 2004).
Far less evident is the application of this insight to governance, although wisdom in governance may be readily acknowledged, as with the occasional appointment of advisory bodies (Committee of Wise Persons of the Council of Europe; Committee of Wise Men on the Regulation of European Securities Markets), and solicitation of the wisdom of others deemed especially wise (The Elders). It is indeed unclear how many levels of skill in governance can be usefully distinguished, however these may culminate in the "wise governance" for which strategic sustainability presumably calls.
Arguably a degree of recognition of these distinctions is indicated by the traditional symbolic role of the sceptre (Embodying the essence of governance in ritual dynamics with mace, sceptre, fasces or vajra? 2021; Integrative "orbital" implications: Crown and Sceptre / Sahasrara and Axis Mundi, 2020).
Far more evident is the recourse to arrays of symbolic "pillars" in the articulation of strategies by intergovernmental institutions (Fundamental values and strategic pillars, 2008; Holders of value configurations -- and their "pillars", 2008; Coherent Value Frameworks: Pillar-ization, Polarization and Polyhedral frames of reference, 2008). For example, the European Union has developed various sets of "pillars" that might be understood as the implicit value architecture of a number of strategic initiatives. The EEC was renamed the European Community (EC) upon becoming integrated into the first pillar of the newly formed European Union in 1993. Classic examples include: the Pillars of Ashoka, the Five Pillars of Islam, and the Pillars of Hercules. Less evident however is attribution of distinct levels of significance by inscription at different heights of the pillar.
As an exercise, the following animations are formed by stacking polyhedra selected for the number of vertices associated with each -- rising from 4 at the base to 64 at the top, passing through 8, 16 and 32. These are the numbers which are so fundamental to the binary coding systems of computers -- based on 2n, where n ranges from 2 to 5. A distinct set of examples could be offered based on the number of edges, or the number of faces.
The numerical attributes of each polyhedra in a stack are presented below as an indication of how it might be used to map qualitative attributes values, concepts or strategies, for example.
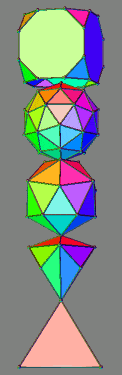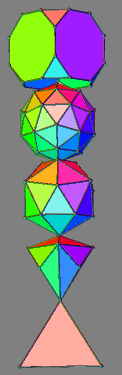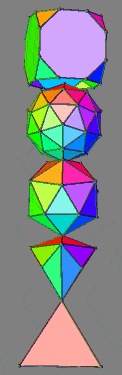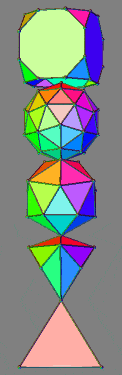
| Stack A alternative renderings | Stack B alternative renderings | ||||
| Non-transparent | Rainbow lighting | Transparent | Non-transparent | Rainbow lighting | Transparent |
 |
 |
 |
 |
 |
 |
| Component polyhedra | Elements (vertices, edges, faces) | Component polyhedra | Elements (vertices, edges, faces) | ||||||||||||
| V | E | F | EV | EF | VF | EVF | V | E | F | EV | EF | VF | EVF | ||
| 42-Rit proj | 64 | 96 | 64 | 160 | 160 | 128 | 224 | 19-Tat proj | 64 | 112 | 48 | 176 | 160 | 112 | 224 |
| rhombic triacontahedron | 32 | 60 | 30 | 92 | 92 | 122 | 182 | pentakisdodecahedron | 32 | 90 | 60 | 122 | 150 | 92 | 182 |
| simplest torus | 16 | 28 | 12 | 44 | 40 | 28 | 56 | 1-freq. trunc. tetra. geodesic sphere | 16 | 42 | 28 | 58 | 70 | 44 | 86 |
| cube | 8 | 12 | 6 | 20 | 18 | 14 | 26 | triakistetrahedron | 8 | 18 | 12 | 26 | 30 | 20 | 38 |
| tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 | tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 |
There is an obvious case for including the truncated icosahedron in such a stack. As the stitching pattern for the standard association football, known world wide, it must necessarily be of a fundamental significance as yet to be fully appreciated, as discussed separately (Game ball design as holding insight of relevance to global governance? 2020). It is especially intriguing in that it is a 32-fold pattern which is so familiar, being much more complex than the 8-fold and 16-fold patterns preceding it in the stack. Potentially more intriguing is the pattern of 64 vertices in the polyhedron which follows it -- being so complex that it can only be represented as the 3D projection of a structure in 4D.
The pillar-like structure of the FIFA World Cup is presented below as holding the aspiration with which the 32-fold pattern is associated. It can perhaps be compared with a cup whose form is so fundamental to religious ceremonies, itself inviting structural insights (Complementary visual metaphors of "Chalice", 2011; In-forming the Chalice as an Integrative Cognitive Dynamic, 2011). Such designs can be explored as echoed in the forms selected to reflect the culmination of strategic endeavour through traditional iconographic use of the laurel wreath (Game-playing, bull-leaping and laurel wreaths, 2014; Winged logos, laurels and strategic uplift, 2020). The animation below left is an exercise in representing nested significance.
| Stack C alternative renderings | Compact visual analogues to vertical arrays | ||||
| Non-transparent | Rainbow lighting | Transparent | FIFA World Cup | Chalice cup | Laurel wreath |
 |
 |
 |
 |
 |
 |
| Component polyhedra | Elements (vertices, edges, faces) | ||||||||||||||
| V | E | F | EV | EF | VF | EVF | xxx | xxx | |||||||
| 42-Rit proj | 64 | 96 | 64 | 160 | 160 | 128 | 224 | ||||||||
| truncated icosahedron | 60 | 90 | 32 | 150 | 122 | 92 | 182 | ||||||||
| cubes-2 | 16 | 24 | 12 | 36 | 36 | 36 | 52 | ||||||||
| triakistetrahedron | 8 | 18 | 12 | 26 | 30 | 20 | 38 | ||||||||
| tetrahedron | 4 | 6 | 4 | 10 | 10 | 10 | 14 | ||||||||
Nested and cage-like polyhedral configurations implying degrees of implicate order
Traditional symbolic configurations: One provocation to further exploration derives from the mysterious function of the so-called Roman dodecahedron. This is a small hollow object made of bronze or stone (4-11 centimetres in diameter). Of dodecahedral form, it has twelve flat pentagonal faces, each face having a circular hole of varying diameter in the middle, the holes connecting to the hollow center. Over a hundred of these have been found across Europe, dating from the 2nd or 3rd centuries AD.
As discussed separately, they have evoked speculation of every kind as to their function -- with no conclusion (Roman dodecahedron, Chinese puzzle balls and Rubik's Cube? 2018). They can be usefully compared with carved stones balls (petrospheres) dating from the Neolithic period, and with the carved Chinese puzzle balls.
| Roman dodecahedron | Chinese ivory puzzle ball | Neolithic carved stone ball | Polyhedral model of solar system of Johannes Kepler on Mysterium Cosmographicum(1596) |
 |
 |
 |
 |
| By Lokilech [GFDL, CC-BY-SA-3.0 or CC BY-SA 2.5 ], from Wikimedia Commons |
British Museum [CC BY 2.0 ], via Wikimedia Commons |
National Museums of Scotland, via Wikimedia Commons |
Reproduced from Wikipedia entry |
The animation of the array of 12 Archimedean polyhedra (in its collapsed form) suggested the further possibility of emulating the classical Chinese puzzle balls, or mystery balls (hsiang ya ch'iu or hsiang ya qiu). As a traditional gift to the Emperor, these were carved out of a single piece of ivory, but now from synthetic ivory, resin, wood, jade, and other materials (Rotation and pumping of nested Chinese "puzzle balls" as symbolizing "worlds-within-worlds", 2015).
They are called "puzzle balls" due to the mystery and puzzling explanation behind their making. There is the possibility of manipulating the inner balls so that their holes align with the outer balls, thereby "solving" the puzzle in a technical sense.
They consist of a number of concentric spheres -- typically from 3 to 7 -- which rotate freely with respect to one another. The sequence of balls is understood to represent the cosmos -- a symbolic reference to the sense of "worlds-within-worlds" as being the very nature of reality. Every sphere has distinctive symbolic carvings, usually of plants and animals. Most often, the outermost will either depict two duelling dragons, or hold a dragon (emperor/male), and a phoenix (empress/female), battling for hold upon the world and keeping it in balance, namely as representations of yin and yang. The most complex known is made of 42 spheres enclosing one another.
Representation of implicate order? As a theoretical physicist, David Bohm is concerned with the illusory nature of fragmentation and the manner in which distinct fragments emerge from wholeness in movement (Wholeness and the Implicate Order, 1980). As discussed separately, Bohm sees the perceptual problems with which he deals as being as relevant to a more healthy response to psychosocial fragmentation as to the problems of fundamental physics (Wholeness and the implicate order, 1983; Coexistence of variety: an implicate order? 2011).
Basing his investigations on insights from the current state of physics, Bohm:
- focuses "on the subtle but crucial role of our general forms of thinking in sustaining fragmentation and in defeating our deepest urges toward wholeness or integrity" ( p. 3)
- arrives at the conclusion that "our general world view is itself an overall movement of thought, which has to be viable in the sense that the totality of activities that flow out of it are generally in harmony, both in themselves and with regard to the whole existence". (p. XII)
- This view implies that "flow is, in some sense, prior to that of the 'things' that can be seen to form and dissolve in this flow". (p. 11)
- Thus the "various patterns that can be abstracted from it have a certain relative autonomy and stability, which is indeed provided for by the universal law of the flowing movement". ( p. 11)
In his challenge to prevailing views, Bohm notably articulated an understanding of holomovement as a key dynamic in quantum mechanics relating explicate and implicate order. (David Peat, David Bohm, Implicate Order and Holomovement, Science and Nonduality; The Cosmic Plenum: Bohm's Gnosis: The Implicate Order).
Any pointers suggestive of the relation between explicate and implicate order are therefore of value, as exemplified by the following indicative of patterns of change implied by by nesting, packing, and transforming symmetrical polyhedra (Psychosocial Implication in Polyhedral Animations in 3D , 2015)
| Indications of cage-like and nesting polyhedral frameworks | |
| Cuboctahedral array of 12 Archimedean polyhedra (around an omitted 13th at the centre; totalling 984 edges, 558 vertices, 452 faces) |
Nesting 5 Platonic polyhedra octahedron, icosahedron, dodecahedron, tetrahedron, cube with Rhombic triacontahedron (green) as a nesting framework |
 |
 |
| Virtual reality variant (.wrl) | virtual reality variants static: vrml or x3d; mutual rotation: vrml or x3d; "pumping": vrml or x3d; videos: "pumping" mp4; "rotation" mp4 |
| Developed with X3D Edit and Stella Polyhedron Navigator | |
| Screen shots of animation of cuboctahedral array of 12 Archimedean polyhedra collapsing into centre (without indication of the 13th at the centre, namely the truncated tetrahedron) |
|
 |
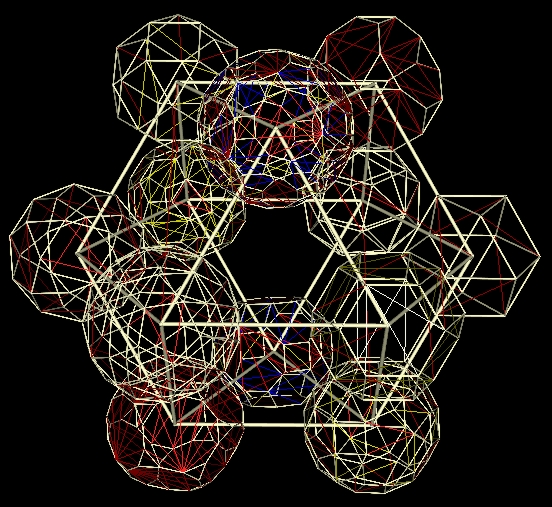 |
| Contextual cuboctahedron rendered partially transparent Video (.mpg; .mov); virtual reality (.wrl; .x3d) |
Wireframe version with all faces transparent Video (.mp4; .mov); virtual reality (.wrl; .x3d) |
| Animations prepared with the aid of Stella Polyhedron Navigator | |
Particular coherence of 60-fold organization? The potentially fundamental implication for cognitive organization associated with the truncated icosahedron in the design of the association football (as noted above) merits further consideration in the light of the role of that polyhedron in the organization of a complex molecule only recently discovered. The molecule is that of C60, named after Buckminster Fuller as buckminsterfullerene. It has a cage-like fused-ring structure made of twenty hexagons and twelve pentagons, therefore resembling a soccer ball. It is the most common naturally occurring fullerene, also existing in space.
Given the contrast with the organization of carbon in organic molecules so fundamental to life, there is a case for exploring psycho-social implications of the polyhedral fullerenes for coherence, integrity and identity of a higher order (Sustainability through Global Patterns of 60-fold Organization:, 2022). The case is all the stronger, in the light of the higher dimensionality of the hypercube, given potential cognitive implications of other game balls, as noted by Michael Deza:
While C60(Ih) is a soccer ball, C70(D5h) and C84(D2d) respectively resemble a rugby and a baseball ball... Can we embed into a hypercube the graph formed by the vertices and the edges of a fullerene (and other chemically relevant polyhedra) while preserving, up to a scale, the path distances? (Fullerenes and coordination polyhedra versus half-cube embeddings, Discrete Mathematics, 1998)
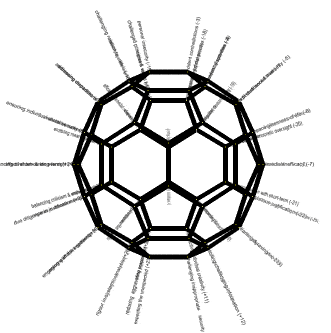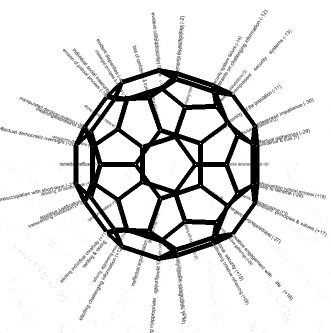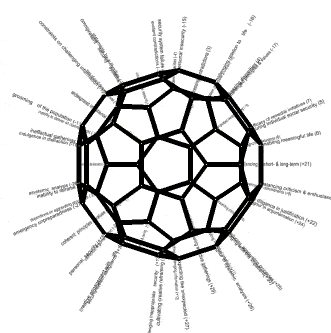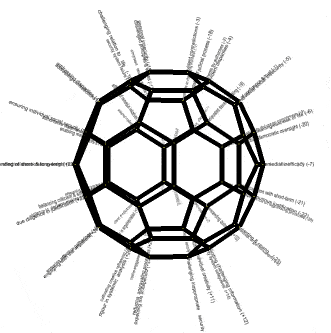
For example, 30 positive and 30 negative global trends can be identified (Convergence of 30 Disabling Global Trends, 2012). These can be suggestively mapped onto a 60-vertex truncated polyhedron, as shown in alternative renderings below. That on the right is a screen shot of the Interactive Mapping of 30 Problems with 30 Strategies onto Truncated Icosahedron using Force-directed Layout (2022). The blue nodes are challenging problems and the orange nodes are remedial strategies -- the titles becoming evident on mouseover. More skillful renderings are suggested in the visual representation of both alternatives.
| Indicative mapping onto 60 vertices of a truncated icosahedron of 30 disabling trends with 30 remedial trends (arbitrary mapping for illustrative purposes) |
||
 |
 |
 |
| Animations made using Stella Polyhedron Navigator | Mapping with force-diected layout (interactive version) | |
Implicate order through hypercube and drilled truncated cube?
The justification for cage-like arrays can be clarified in the light of the recourse of logic, especially oppositional logic, to use of the hypercube (or tesseract) to represent the 16 Boolean connectives as operators of significance to computer operations (Reframing forms of connectivity through the logic of oppositional geometry, 2020). These are variously illustrated in the following images.
As explained by Steven H. Cullinane (The Geometry of Logic: finite geometry and the 16 Boolean connectives, Finite Geometry Notes, 2007), a Hasse diagram of a Boolean lattice, may also be viewed as a tesseract (4-dimensional hypercube). The vertices represent the 16 traditional "binary connectives". The tesseract's 16 vertices may also be regarded as representing either the 16 subsets of a 4-set or the 16 elements of the affine 4-space A over the two-element Galois field. The pattern was originally depicted by Shea Zellweger, as a "logic alphabet", as shown below.
The images below show various attempts to facilitate comprehension of 4-dimensionality suggested by a central nexus. The animation of a hypercube (tesseract) on the right is very helpful in suggesting the necessarily paradoxical interplay of the alternation between an inner and an outer perspective.
| Contrasting representations facilitating comprehension of 4-dimensionality and a central nexus | |||
| Cubic configuration of BaGua trigram symbols by Z. D. Sung |
Logic Alphabet Tesseract |
Topological 4-statement Venn diagram (graph of edges of a 4-dimensional cube as described by Tony Phillips) |
Tesseract animation simulating requisite 4-dimensionality? |
 |
 |
 |
 |
| Reproduced from Z. D. Sung, The Symbols of Yi King or the Symbols of the Chinese Logic of Changes (1934, p. 12) | Diagram by Warren Tschantz (reproduced from the Institute of Figuring) . |
A vertex is labeled by its coordinates (0 or 1) in the A, B, C and D directions; the 4-cube is drawn as projected into 3-space; edges going off in the 4th dimension are shown in green. | by Jason Hise [CC0], via Wikimedia Commons |
The literature of oppositional logic for the representation in truth tables of the 16 Boolean connectives (as indicated in the above hypercube representation in 4D) reduces them to 14, notably to enable their geometrical representation in 3D (Oppositional logic and its geometry -- 16 minus 2 connectives?, 2021;
From 16 to 14 connectives -- precluding a logical meta-perspective? 2021; Questionable confusion in configuring strategic frameworks: "fudging" self-reflexivity? 2019). A key polyhedron used to map the 16 (-2) Boolean logical connectives in that approach is the rhombic dodecahedron of 14 vertices and 12 faces.
The focus on a 14-fold configuration indeed offers significant insight (Pattern of 14-foldness as an Implicit Organizing Principle for Governance? 2021). However there is also potentially a case for exploring the value of 16-fold arrays (Deprecation of potential correspondences: 16-fold patterns? 2019).
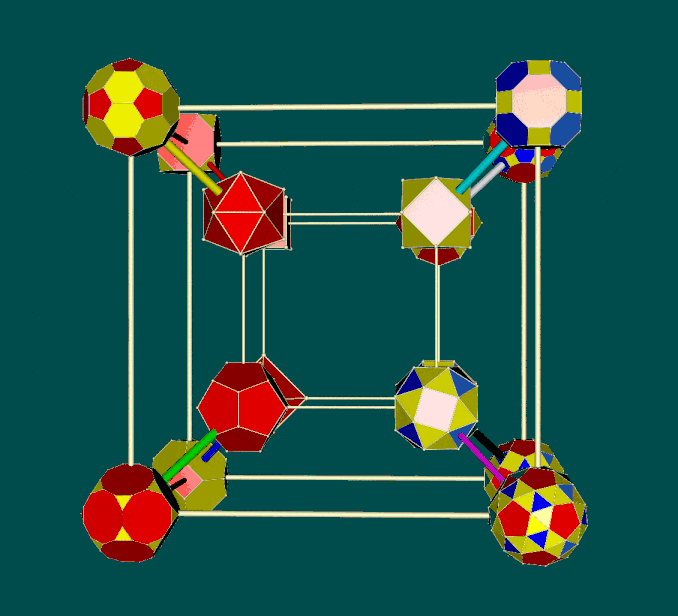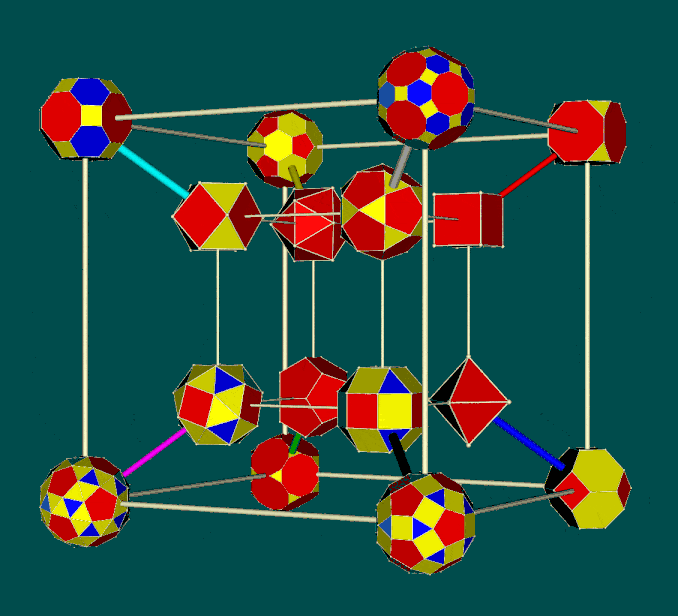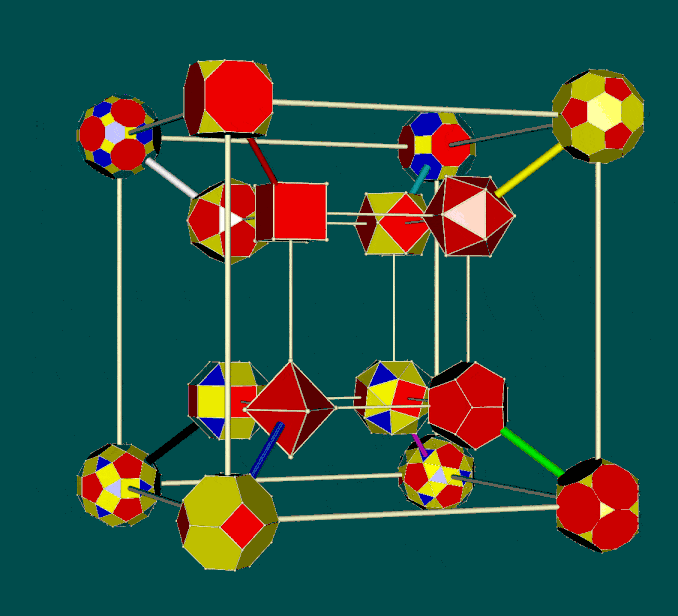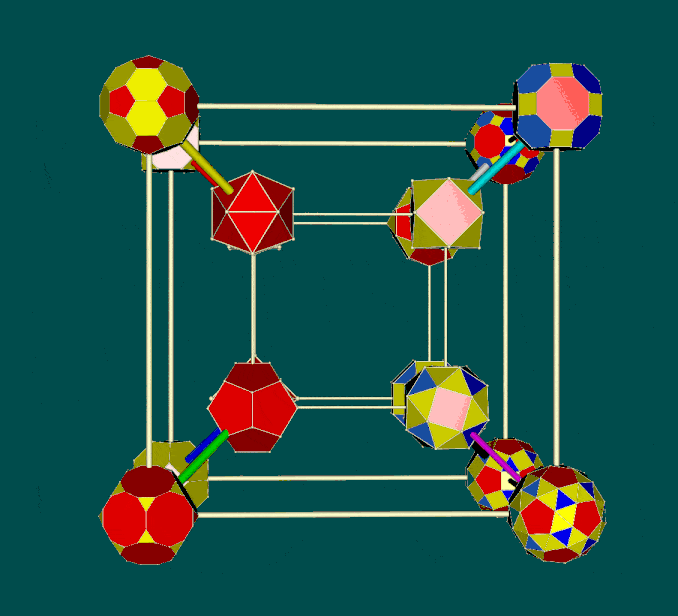
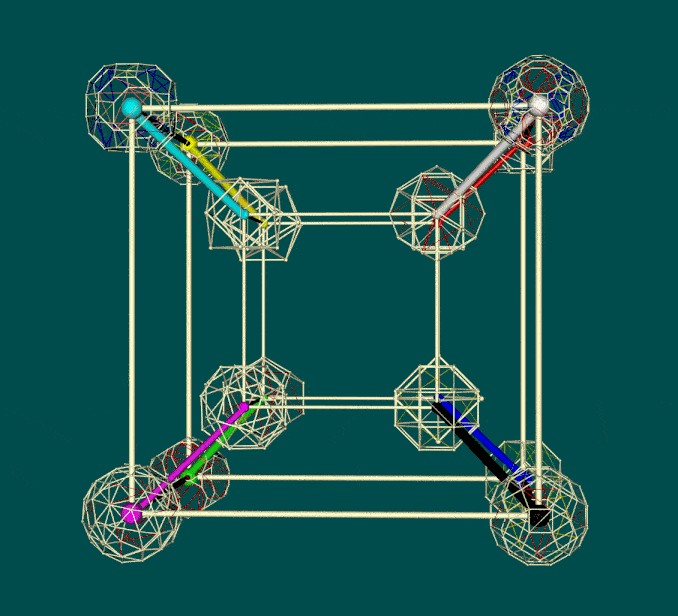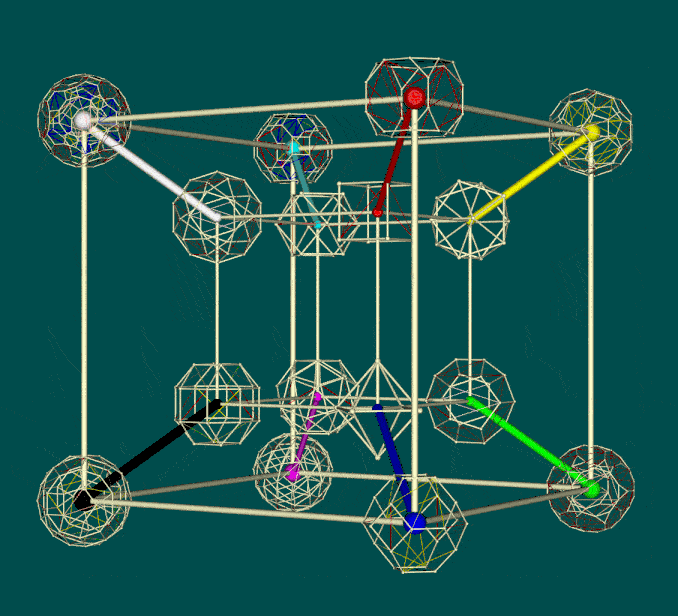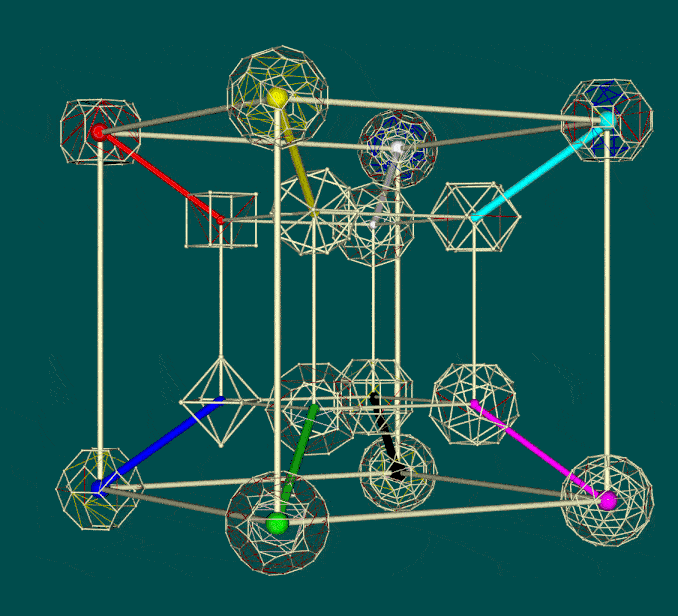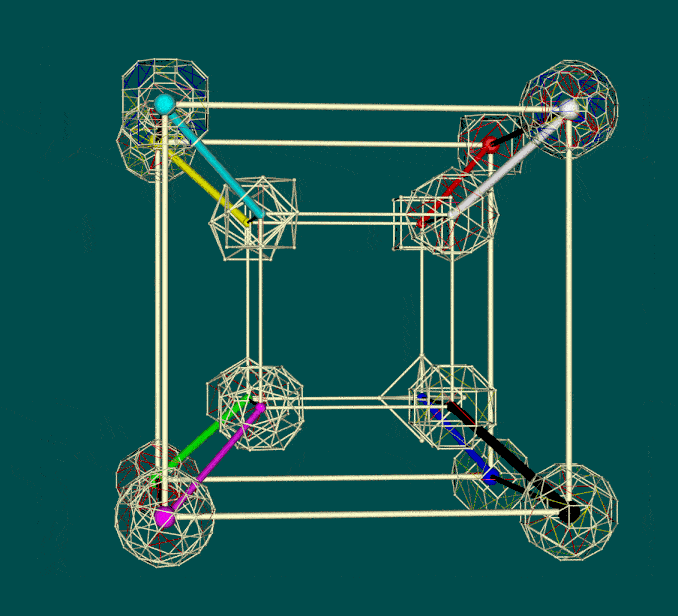
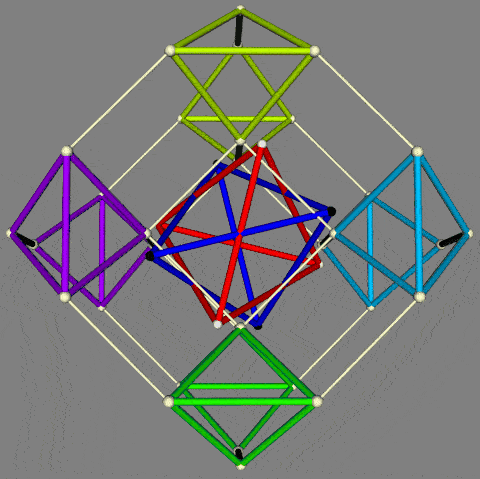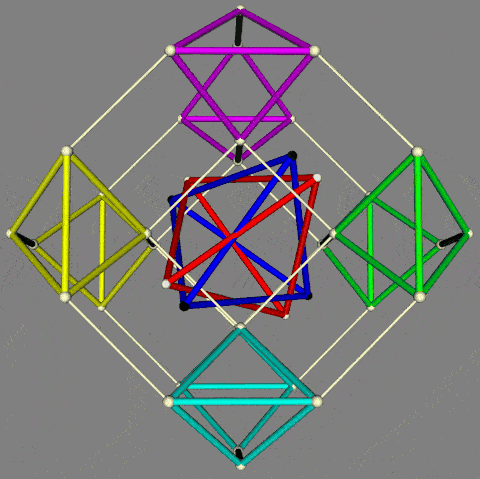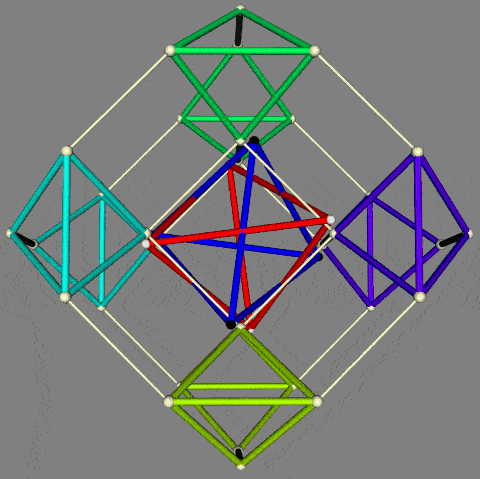
In the light of Critchlow's arrangement of 12 semi-regular Archimedean polyhedra (as noted above), there is a case for exploring an arrangement of such polyhedra on a hypercube -- if only for mnemonic purposes. Noting that Critchlow's closest packaging array is centered on the truncated tetrahedron (the 13th Archimedean solid), it can be assumed for the purposes of the exercise that the tetrahedron can be omitted from the set of 5 Platonic polyhedra. This then enables a total of 16 polyhedra to be arrayed as a hypercube. The 4 Platonic polyhedra can be positioned on vertices of the inner cube, together with 4 of the Archimedean polyhedra -- of which the remaining 8 can then be positioned on the outer cube (as variously shown below).
Of particular mnemonic interest is the possibility that the polyhedra can be judiciously placed to reflect the symmetry-preserving operations of the Conway relational chart (reproduced above). As one initial effort in this respect, those polyhedra on vertices of the outer cube are primarily truncations of those on the inner cube.
| Configuration of 16 Platonic and Archimedean polyhedra on a hypercube (not to scale) |
||
| Solid faced | Names (see variants below) | Transparent faces |
 |
 |
 |
| Animations made using X3D- Edit and Stella Polyhedron Navigator | ||
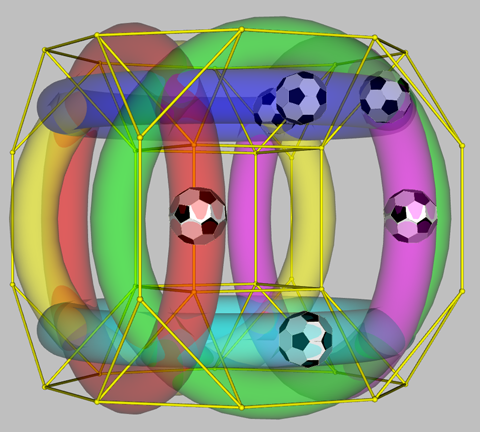
Drilled truncated cube: The pattern of 64 is nearly unique within the polyhedral context. However one interesting candidate is the toroidal drilled truncated cube with 64 edges -- with which any set of 64 elements could be associated (Proof of concept: use of drilled truncated cube as a mapping framework for 64 elements, 2015). The issue is whether the manner in which they can be positioned on that framework constitutes a configuration which is meaningful in relation to particular cases, such as the 64 genetic codons or the 64 hexagrams of the I Ching.
It is possible that known constraints in the patterning in such particular cases can together offer guidance in the attribution of the distinct elements -- of relevance to each case, as tentatively explored (Changing Patterns using Transformation Pathways, 2015):
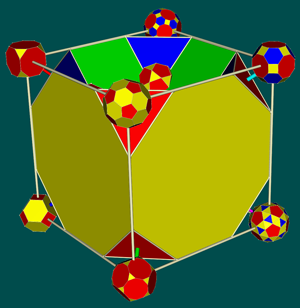
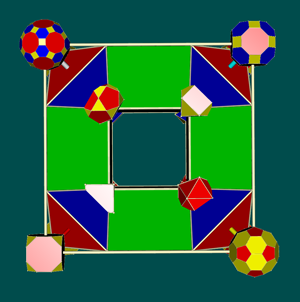
As shown below, of particular interest is the manner in which a cube is effectively "nested" within the drilled truncated cube, as in the case of the hypercube above (Psychosocial Implication in Polyhedral Animations in 3D, 2017). The pattern invites a variety of experimental interactive animations (Dynamics of Parallel edges of Drilled truncated cubes in 3D; Experimental Interactive Display of Cube Edges in Movement in Virtual Reality.
| Alternative views of hypercube (as above) nested within drilled truncated cube | ||
 |
 |
 |
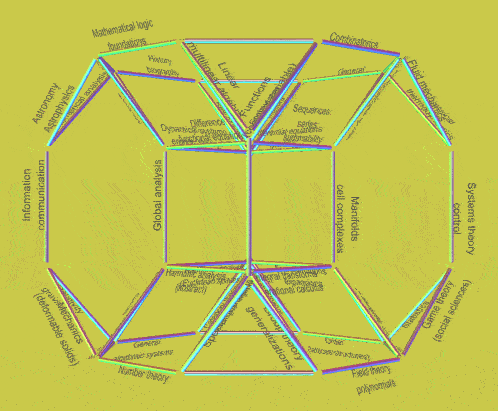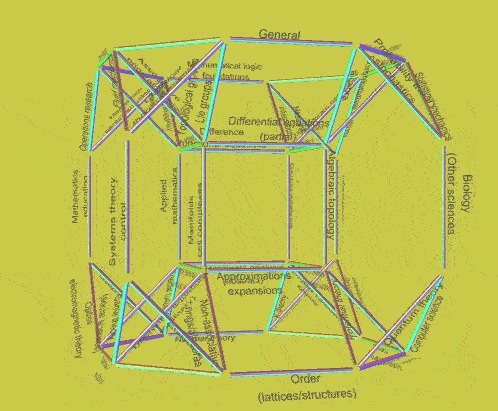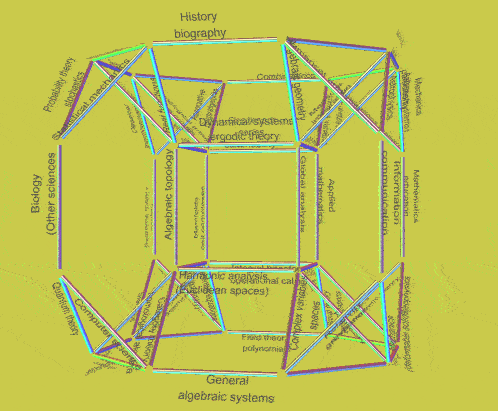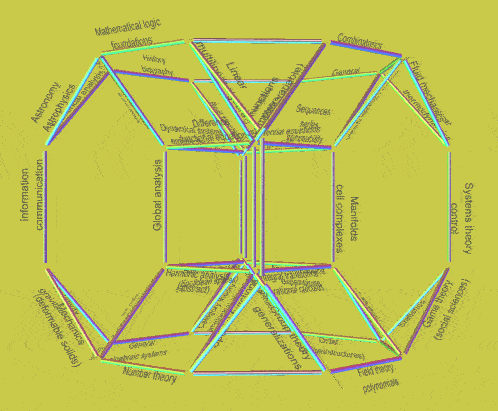
An earlier experiments explored the use of that polyhedra for other mapping purposes (Configuring the 64 subjects of mathematics as a 64-edged drilled truncated cube, 2021). There its use was suggested for ordering the dynamics within a pantheon (Exploring potential dynamics within a pantheon?, 2021). The following examples are reproduced from a discussion in Enabling Wisdom Dynamically within Intertwined Tori: requisite resonance in global knowledge architecture (2012).
| Experimental mappings with drilled truncated cube of 64 edges | ||
| Animation with faces non-transparent (mapping 64 genetic codons) |
Animation with faces transparent (mapping 64 mathematical subjects) |
Animation with faces transparent (mapping 64 I Ching hexagrams) |
 |
 |
 |
| Animations prepared using Stella Polyhedron Navigator | ||
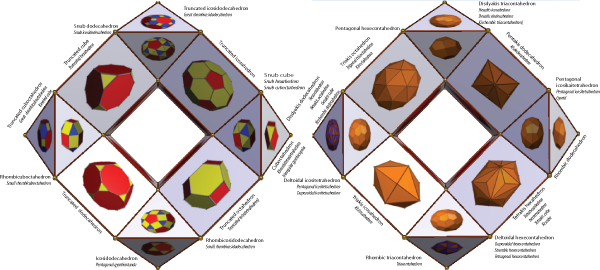
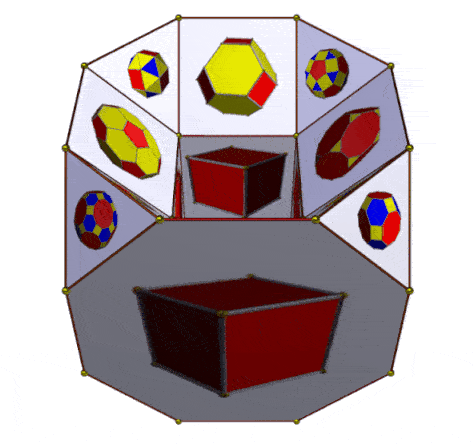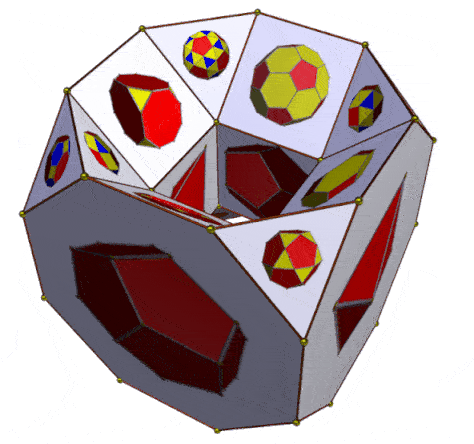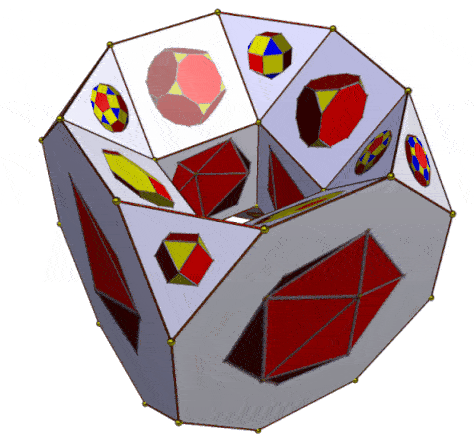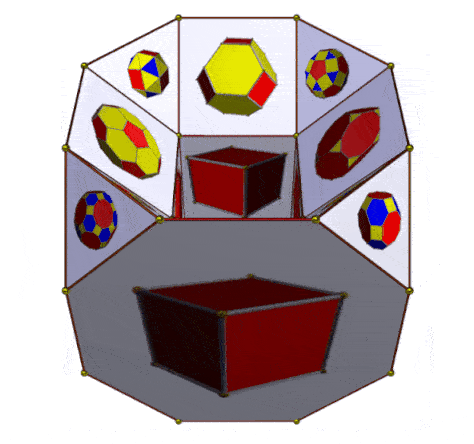
Following the experimental configuration of 16 Archimedean and Platonic polyhedra on a hypercube (as illustrated above), and on the assumption that a hypercube can be mnemonically embedded within a drilled truncated cube, a further presentation of a 16-fold array can be explored. However, given that the drilled truncated cube has 32 faces, 16 can indeed be used for the Archimedean and Platonic polyhedra, but the remaining 16 faces can be used for the geometric duals of those polyhedra. In the case of the Archimedean polyhedra, these are the Catalan polyhedra. The duals of the Platonic polyhedra are themselves Platonic polyhedra (Duals of Platonic Solids, Wolfram Demonstration Project).
The images below position the 12 Archimedean polyhedra on 12 visible faces of the drilled truncated cube such as to correspond to the 12 Catalan polyhedra on the remaining 12 faces (on the reverse of the drilled truncated cube). Not shown in the images below, being only apparent in the animations which follow, are the 4 Platonic polyhedra (on the outer sides of the cube) and their duals on the corresponding inner surfaces of the cube).
| Attribution of 12 Archimedean and 12 Catalan polyhedra on a drilled truncated cube (4 Platonic polyhedra, with their 4 duals are not shown) |
 |
| Alternative animations of drilled truncated cube showing 16 Archimedean and Platonic polyhedra and their 16 duals (names in image above, with variant names) |
||
 |
 |
 |
| Animations prepared using Stella Polyhedron Navigator | ||
| Images suggestive of other design metaphors | ||
| Unfolding of drilled truncated cube with polyhedra and duals (as above) |
Wire frame of dual of drilled truncated cube |
UN Art Installation in Tblisi, Georgia on Rubik's Cube |
 |
 |
 |
| Animations prepared using Stella Polyhedron Navigator | Reproduced from UNIC@Work, October 2016 - Special UN Day Bulletin | |
Polyhedral representation of Sustainable Development Goals including "Own Goals"?
As indicated by the suggestive depiction of the UN Sustainable Development Goals on Rubik's Cube (above right), there is a case for imaginative exploration of alternative means of depicting the iconic images of the goals (Interplay of Sustainable Development Goals through Rubik Cube Variations: engaging otherwise with what people find meaningful, 2017). One approach is to use 16 of the goals (omitting the 17th as coordinative) and associate them with 16 faces of the drilled truncated cube as shown below.
This usefully evokes the judicious possibility of their placement to suggest systemic relationships between them. The edges between the faces are then indicative of some form of confrontation, feedback or challenge, with the vertices potentially indicative of trilemmas.
Correspondences between the faces also enables the polyhedron to be used as a means of indicating the tendency to fail in achievement of the goal -- perhaps to be understood globally as some form of civilizational "own goal" or "self-goal" (Variety of System Failures Engendered by Negligent Distinctions , 2016).. For this purpose, 16 of the icons have been coloured black and appropriately placed. [NB: The software used reverses images in certain positions, potentially suggestive of strategic misunderstanding -- until this is corrected.] It is appropriate to reflect on the inability to provide a coherent global overview of the set as displayed -- and hence the value of the animations on different axes below, in each case obscuring the icons at each extreme of the axis selected. Other design metaphors could of course be envisaged, including shading the "own goals" to varying degrees as an indication of remedial success.
| Experimental polyhedral representation of Sustainable Development Goals of the UN (SDGs) | ||
| Use of 32-sided drilled truncated cube to represent 16 SDGs and 16 corresponding "own goals" | ||
 |
 |
 |
| Animations prepared using Stella Polyhedron Navigator | ||
Toroidal polyhedral ring array
The drilled truncated cube is recognized as approximating a torus. The argument can be developed further given recognition that fullerenes of carbon can take toroidal form (as mentioned above). This can be related to exploration of its psychosocial implications (Imagining Toroidal Life as a Sustainable Alternative: from globalization to toroidization or back to flatland? 2019).
A spreadsheet application has been developed by Sergey Bederov of Cortona3D to explore the possibility of a potentially more stable toroidal fullerene (Toroidal fullerenes as a complement to the global form, 2022). This introduces pentagons in accordance with research on toroidal carbon nanotubes (Florian Beuerle, et al, Optical and Vibrational Properties of Toroidal Carbon Nanotubes, Chemistry: a European Journal, 17, 2011, 14; Pakhapoom Sarapat, A Review of Geometry, Construction and Modelling for Carbon Nanotori, Applied Sciences. 9, 2019, 11). Such research recognizes that in order to maintain their Euler characteristic (zero for a torus), an equal number of heptagons (7-gons) needs to be added (coloured blue and red in the screen shots below to distinguish them by size). Whether pentagons or hexagons, these are in each case by hexagons; mathematically all vertices lie on a perfect torus and edge lengths differ by only 24%.
| Screen shots of a toroidal fullerene with pentagons and heptagons surrounded by hexagons | |
 |
 |
| Screen shots derived from a 3D model kindly developed by Sergey Bederov of Cortona3D. X3D model | |
Such experiments suggest the possibility of configuring the 12 Archimedean polyhedra together in the form of a ring as variously illustrated below -- in relation to a torus of otherwise. Alternatives could use the Catalan variants.
| Configuration of 12 Archimedean polyhedra in relation to a torus | ||
 |
 |
|
| Animations prepared using X3D Edit and Stella Polyhedron Navigator | ||
Such a configuration is consistent with earlier exercises focusing on the design metaphor of an archetypal Round Table -- together with its numeric relationship to the Last Supper and the communication issues implied by both:
- Increasing the dimensionality of the archetypal Round Table? (2018)
- Implication of the 12 Knights in any Strategic Round Table (2014)
- Clarifying the Unexplored Dynamics of 12-fold Round tables (2019)
- Dialogue: towards the dynamics of the archetypal "Round Table"? (2011)
The strategic focus on 12-fold patterns suggests that these are intuitively recognized as representing 12 distinctive compromises between unity and diversity -- exemplified by their various approximations to a sphere as the set of semi-regular Archimedean polyhedra. The challenge of the 13th is evident in various forms. The relation to the 5 more regular Platonic polyhedra is another matter.
Dynamics of systemic connectivity as a challenge to invariance
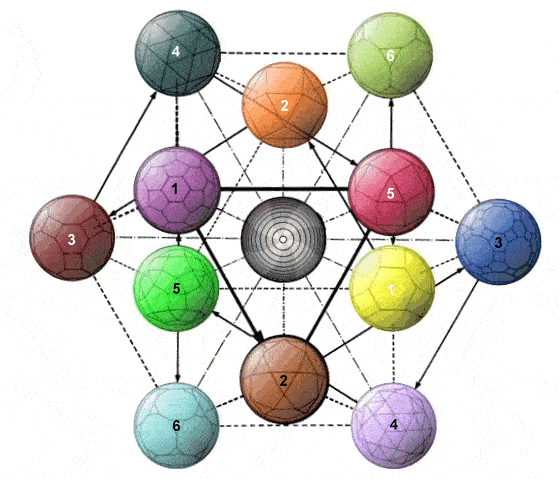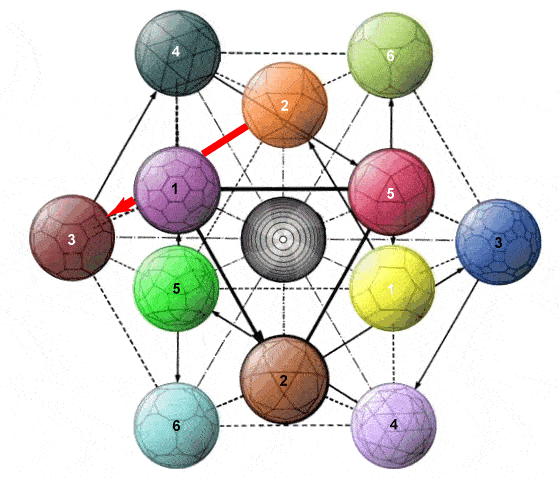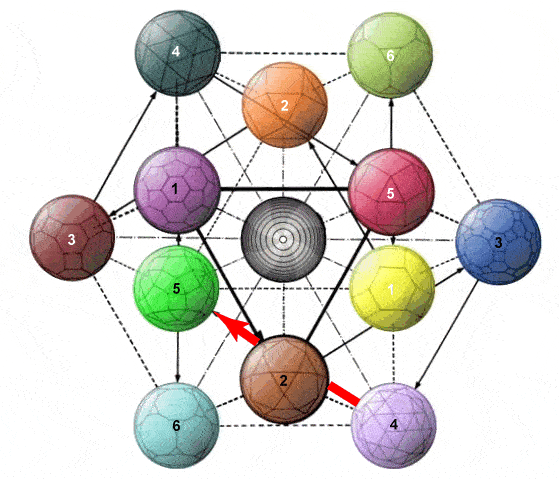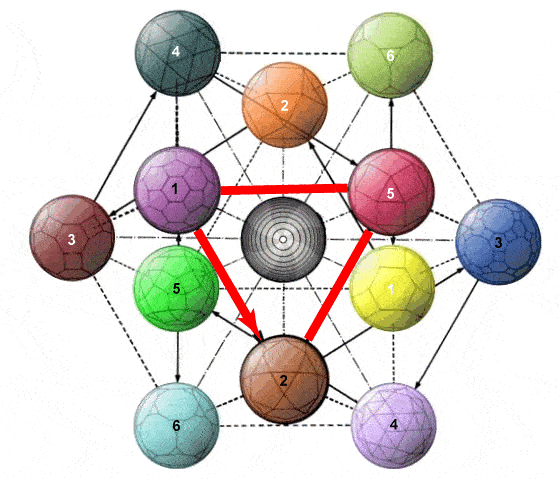
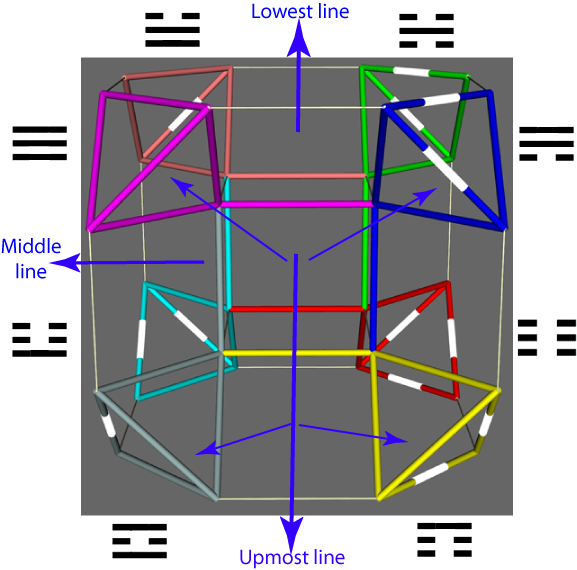
Towards attribution of cognitive significance to complex patterns: It is one thing to elaborate complex symmetrical structures as an indication of potentially significant coherence. It is quite another matter to articulate a large array of distinctions and associate them meaningfully with features of that structure as a mnemonic aid. In this respect the Chinese binary coding system which inspired Gottfried Leibnitz merits attention (Mary von Aue, How the 'I Ching' Inspired His Binary System, Inverse, 2 July 2018). It was presented to him 1701 in the form of the Shao Yong circle of 64 hexagrams -- of which an adaptation is presented below right, and discussed separately in the light of its recognized capacity to order the 64 genetic codons (Changing Patterns using Transformation Pathways, 2015).
Of interest in relation to the drilled truncated cube is the manner in which the 64 hexagrams are traditionally clustered in 8 "houses" on the basis of one of the component trigrams (Organization of I Ching hexagrams in terms of traditional "houses", 1995). The clustering by "house" is evident from the two "houses" in each quarter of the circle (below right). The basic 8 trigrams of the BaGua pattern have been associated with a cubic configuration, as illustrated above (Z. D. Sung, The Symbols of Yi King or the Symbols of the Chinese Logic of Changes, 1934, p. 12). In the image below left the manner in which the lines of those distinctive trigrams are associated with the outer corner features of the drilled truncated cube are shown.
The elements of the second set of 8 distinctive trigrams can be associated below with inner features of each corner. These 8 inner trigrams are then presented dynamically in the central animation below in relation to the 8 static corner elements indicative of the distinctive "house" clusters. Fundamental to the association of significance with the hexagrams is whether they are to be read from top down or from bottom up -- an issue of inner-versus-outer highlighted by the dynamics of the hypercube presented above (Unquestioned Bias in Governance from Direction of Reading? 2016). The animation presents the dynamics of each of the 8 "houses" in the same sequence, as indicated in the circular representation. The dynamics of the structure as a whole thus cycles through all 64 hexagrams.
| Association of traditional circular hexagram encoding with drilled truncated cube in 3D | ||
| Correspondence of trigram coding to 8 corners of drilled truncated cube |
Animation of upper and lower trigrams represented on drilled truncated cube |
Circle of hexagrams surrounded by a circle of codons |
 |
 |
 |
| Interactive 3D variant | ||
Although somewhat simplistic, the use of 3D web technology (X3DOM) in the experimental development of the animation above does demonstrate that it is possible to control separately all the individual elements of the polyhedron as a mnemonic aid. With greater skill, such an animation could be further developed to hold a greater range of significance -- adjusting timing, colours, sound, viewpoint perspectives, and any labelling -- according to interactive and aesthetic preferences. The pattern of attribution of significance could be variously adjusted experimentally. To the extent that the structure can be considered to be a simple model of a "global brain", of interest is the manner in which the polyhedron is segmented into "lobes" -- especially evident when rotated in 3D.
Significance is traditionally attributed to the 64 hexagrams through metaphor, allowing for many adaptations to sustainable dialogue, vision, conferencing, policy, network, community and lifestyle (Transformation Metaphors derived experimentally from the Chinese Book of Changes (I Ching), 1997).
Coherence of sustainable development? An earlier exercise with respect to the SDGs can be seen as anticipating the following argument (Interrelationships between 64 Complementary Approaches to Sustainable Development , 2002). The challenge of systemic coordination and coherence of the 16 SDG goals is indicated by the 17th: Strengthen the means of implementation and revitalize the global partnership for sustainable development . As explained, given its "keystone" role, this goal has been omitted from the 16 mappings above, as with the omission of the tetrahedron and the truncated tetrahedron in the polyhedral configurations.
An interesting design possibility for mnemonic purposes is to position the omitted polyhedra as animations within the inner cube of the drilled truncated cube (as shown below).
| Angled animations of dynamics of tetrahedra and truncated tetrahedra
nested within drilled truncated cube (Screen shots of rotation on vertical axis with solid or transparent faces) |
|||
| Counter-rotating tetrahedron (red) and dual (blue) |
Truncated tetrahedron | Truncated. tetrahedron with dual | |
 |
 |
 |
 |
To the extent that the drilled truncated cube constitutes a potential cognitive Rosetta Stone, inclusion of animations within the form provides a valuable contrast to the stasis conventionally associated with invariant configurations -- and the nature of any "philosopher's stone". Following from the reference above to transmission systems, the rotation of the inclusions is also reminiscent of the fundamental importance of rotation in electromagnetic technology -- namely in motors and dynamos, as developed by Nikola Tesla as noted above (Reimagining Tesla's Creativity through Technomimicry, 2014).
Fundamental to Tesla's innovative discoveries was the rotation of a magnetic field, potentially suggestive of psychosocial analogues (Potential implications of alternation and rotation in psychosocial fields, 2014). This is especially evident in the operation of a commutator in motors and dynamos. in addition to concern with with positive and negative, the insights into operation of electrical systems merit consideration for the operation of psychosocial systems (Electrical Systems as a Guiding Metaphor for Stages of Group Dialogue, 2001). It is intriguing that mathematics uses commutator to give an indication of the extent to which a binary operation fails to be commutative. The challenge of global governance could well be seen metaphorically as one of "commutator design" -- by whatever metaphors this is enabled.
Also of mnemonic value in the case of the tetrahedral animation (left above) is the alternation between a degree of "top-down" and "bottom-up" -- as might be a democratic ideal. The tetrahedron and its dual may be understood as either counter-rotating, or co-rotating then potentially forming a stella octangula (or stellated octahedron). Symbolic significance attributed to this form is discussed separately with other animations, as a 3D version of the Star of David (Framing Global Transformation through the Polyhedral Merkabah, 2017; Polyhedral Merkaba Symbol in Virtual Reality: experimental interactive 3D display).
As with a commutator, the manner in which the vertices of the rotating polyhedra successively contact the surrounding structure is suggestive of how processes of alternation in governance could be understood as variously triggered. The more complex animations below indicate how the four corner parts of the surrounding structure are successively coloured distinctively following such contact, thereby highlighting particular "information pathways" through the structure of categories it might map (as noted above).
| Screenshots of animations of alternative views of tetrahedra rotating within drilled truncated cube (rotation changes colours of external parts in a cycle) |
||
| Co-rotation of central tetrahedra in the form of a stella octangula (stellated octahedron) | Counter-rotation of central tetrahedra | |
 |
 |
 |
| See access to interactive 3D animations below; x3d variant | ||
Technically the animations above, as extracts from a video, are only indicative and are variously unsatisfactory. In particular the phasing of the colour changes is not well-coordinated with the rotation of the central polyhedron -- given that the video and 3D versions emphasize a smooth rotation rather than a step shift in position. Slower speeds may well be far more meaningfully appealing. However, with greater skill, the structure enables further modification to the changing colours, possibly extended from four to eight colours with further segmentation of the structure accordingly. This would be appropriately consistent with preferences for 8-fold organization (Framing Cognitive Space for Higher Order Coherence, 2019; Cubic organization of I Ching trigrams -- an eightfold way, 2019).
Corresponding sound effects could be added, given the case for facilitating complex pattern comprehension through sonification. Such experiments are consistent with arguments made separately (Envisaging a Comprehensible Global Brain -- as a Playful Organ , 2019). Another intriguing possibility is to use 3D web technology to enable "rays of light" to pass between facets of a structure with rotating elements, as an indication of information pathways and connotations -- thereby potentially enhancing memorability in aesthetic terms. Visualization of the interplay of sets of voices in discourse (24-fold Pattern Implied by Dynamics of the Lauburu in 3D, 2016).
Usefully reframing the stasis implied by the "philosophers stone" is the forgotten chess-like game Rithmomachia (The Battle of Numbers), which combined the pleasures of gaming with mathematical study and moral education (Ann E. Moyer, The Philosophers' Game: rithmomachia in Medieval and Renaissance Europe, 2001). Complexifying the framework of a simple abacus, the drilled truncated cube evokes the possibility of a framework in 3D for such a game (as with three-dimensional chess) -- with the aesthetic and cognitive connotations evoked by Hermann Hesse (The Glass Bead Game, 1943).
Categories "enstoned" and the myth of invariance? There is an unquestioned assumption that the most fundamental categories are metaphorically "set in stone" -- implying a degree of stasis which could be understood as contrary to their fundamental nature, especially when associated with a cube. Challenges to this assumption from the perspective of experiential reality can be variously explored (Fivefold Clustering of Ways of Being Stoned, 2012). The latter distinguishes between:
- Enstoning through imagination, dreams, drugs and imbibing
- Enstoning of promise, potential, possibility and pattern
- Enstoning with rocks and rockets
- Enstoning in memorials and monuments
- Enstoning through petrification and entombment
In the preceding discussion of the articulation of the traditional 7-fold set of values/virtues deemed fundamental to society, animations were presented using a cubic framework (Global ethical nexus of disparate challenges, 2002). This used a cube to offer a means of representing the dynamics by which 7 "axes of bias" could be distinctively explored. Clearly such a cube could be recognized as central to that framed by any hypercube-like structure, as discussed separately (Eliciting the dynamics of the cube: reframing discourse dynamics, 2018; Mark Ronan, The Rotations of a Cube; The Rotational Symmetries of the Cube, York University).
As with an indicative animation of a hypercube presented above, its paradoxical nature is further explored there through the seemingly impossible inversion of a cube. The drilled truncated cube also invites exploration of its potential dynamics and visualization (Decomposition and recomposition of a toroidal polyhedron -- towards vortex stabilization? 2015; Dynamics of movement of parallel edges of drilled truncated cube).
Other dimensions to the mapping potential of the drilled truncated cube follow from the fact that its 32 faces are of 5 types, its 64 edges are of 9 types, and its 32 vertices are of 4 types. These are each associated with extensively explored patterns of significance to quite disparate domains. The following section explores the use of other polyhedral configurations, especially with respect to the ring configuration associated with the 12-fold pattern, as noted above. As the animations above make clear, one particular perspective on the drilled truncated cube highlights a 12-fold pattern. framed by two distinctive 4-fold patterns thereby offering a 20-fold pattern (referenced above).
Intriguingly the ambiguity associated with "invariance" of fundamental categories has been explored by the musicologist Ernest McClain (Myth of Invariance: the origins of the gods, mathematics and music from the Rg Veda to Plato, 1976).
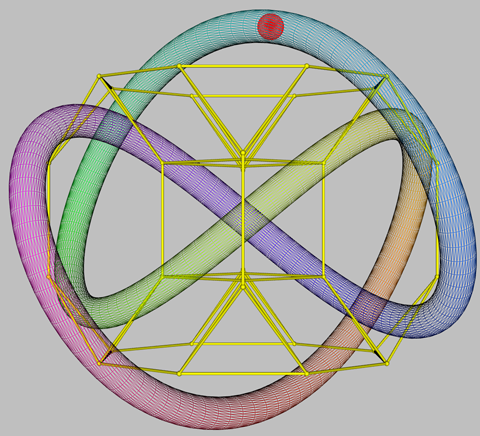
Cognitive dynamics through cycles of flow: Symmetry within the drilled truncated cube suggests its use in framing distinctive toroidal rings indicative of contrasting modes and orientations of flow. These can be understood as a a contrasting expression of dimensions otherwise taking the form of axes. Thus that on the left can be understood as relating the extremes of horizontal axes and diagonal axes. That in the centre is indicative of the manner in which the central cube is framed by 6 distinctive flows.
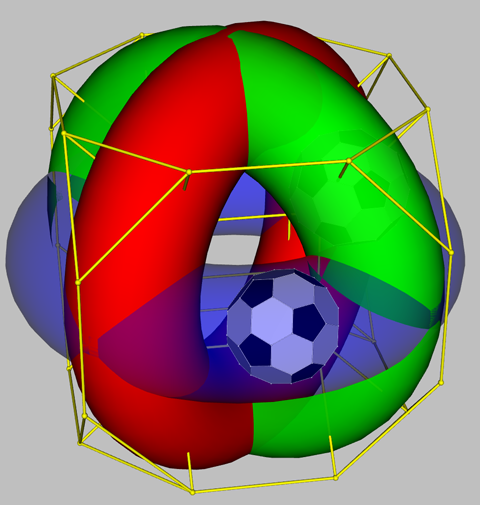
The animation on the right is an experiment on the assumption that the Mereon toroidal knot, with which fundament significance has been associated, might indicate a mode of glow through the cubic form in some manner. The knot features in earlier commentary (Cyclic Representation of Coherence as Knots and Otherwise , 2022; Louis Kauffman, Pattern, Sign and Space: Mereon Thoughts. 2003; Louis H Kauffman, et al, The Mereon Matrix: everything connected through (k)nothing, 2018).
The toroidal presentation evokes consideration of what could be variously understood as "flowing" in a cognitive cycle (Circulation of the Light: essential metaphor of global sustainability? 2010). The "cognitive locus" can then be represented by a sphere (as on the left) or as a spherical polyhedron (as with use of the truncated icosahedron in the other animations below). This follows from the experiment above in which all the Archimedean polyhedra flow through a torus -- thereby suggesting the variety of perspectives or cognitive phases in play around an archetypal roundtable. Use is made below of the truncated icosahedron because of its familiarity as a soccer ball with all that its dynamics may imply in a game.
Toroidal flow is potentially of the greatest importance with respect to future global energy requirements -- framed by experimental development of toroidal nuclear fusion reactors, most notably that of ITER. To the extent that these invite technomimicry, the animation on the left is potentially suggestive of the operation of a psycho-social analogue -- an Imaginal Transformation of Energy Resourcing (ITER-8) (Enactivating a Cognitive Fusion Reactor, 2006).
Animations indicative of toroidal circuits of interest in relation to the drilled truncated cube |
||
| 3 mutually orthogonal toroidal rings | 6 toroidal rings framing the central cube | Interweaving of Mereon toroidal knot |
 |
 |
 |
| Interactive 3D variant | Interactive 3D variant | Interactive 3D variant |
Cognitive design challenges beyond 64? The transformations from patterns of 4 to 64 are potentially taken further in numerical terms by the animations above. In the case of the 4-sided tetrahedron (with a tetrahedron as its own dual), the 8 sides (or vertices) together extend the 64 edges of the drilled truncated cube to 72 . This anticipates the traditional emphasis on the dynamics of that pattern, as discussed below in various Western traditions. Given the reference above to Jacob's Ladder, its degrees were to the number of 72 (according to the Zohar). The traditional central importance of the 8-edged square pyramid -- architecturally -- offers a similar extension to 72, although questionable in terms of symmetrical elegance.
In the case of the animation of the 18-edged truncated tetrahedron (with its 18-edged dual), the pattern of 64 would be extended by 36 to a 100-fold pattern as variously appreciated. Combining both animations, the pattern of 64 would be extended to 108 -- of considerable significance in the traditions of Buddhism, Hinduism and Jainism.
A design assumption to be explored is how the inner portion of the drilled truncated cube acts as a form of "housing" for a cognitive nexus -- as a metaphorical commutator. Metaphorical alternation could be considered a potential requisite of any function as a cognitive Rosetta Stone -- recognized by physicists to a degree in terms of wave-particle duality and the Uncertainity Principle. The insight is usefully emphasized by the Sanskrit adage Neti Neti (Not this; Not that), suggestive of a fundamental cognitive dynamic and driver. Somewhat ironically this is appropriately challenged by the the insight of Alfred Koryzbski regarding the problematic consequences of assertions of what "is" (Science and Sanity: an introduction to Non-Aristotelian Systems and General Semantics, 1994).
From a design perspective there is a challenging loss of pattern continuity by switching from the focus on 64 edges to dependence on 8 sides of the stella octangula or the tetrahedron and its dual. In terms of cognitive "commutator design", this is only partially remedied by embedding the stella octangula in another cube (again with 8 vertices) nested at an angle within the inner cube (screenshots below, with access to 3D animations). It is appropriate to emphasize that any such fundamental cognitive nexus is necessarily associated with paradox, as explored through the illusory ambiguity of the Necker cube discussed by Steven M. Rosen (Splitting the Atom: the paradox of proprioceptive dialogue, May 2022; The Strange Nature of Quantum Perception: to see a photon, one must be a photon, Journal of Mind and Behavior, 42, 2021, 3-4).
| Indicative animations of "commutator designs" for global governance (preliminary screenshots) |
|
 |
 |
| Interactive 3D variant | Interactive 3D variant |
Strategic implications of traditional angelic and demonic configurations
Contrasting encodings of subtlety? Geometry and polyhedra offer one language by which subtlety and high orders of complexity can be encoded and communicated -- among those who comprehend and appreciate that language (Engaging with Globality -- through cognitive lines, circlets, crowns or holes, 2009). There is a case for emphasizing that that language, is only one of an unexplored range of cognitive modalities by which it is assumed that subtlety can be organized and communicated -- each with advantages and disadvantages for those who prefer one or the other. The abstractions of mathematics and logic, and their possible expression in equations, constitutes another such language particularly challenging for many (Dynamics of Symmetry Group Theorizing: comprehension of psycho-social implication, 2008).
It might be similarly argued that the language of strategic values and problems is appreciated by some with governance preoccupations, whilst being experienced as alienating by others -- including many of scientific orientation. Insights may even be elicited from angelology as a quite distinctive cognitive modality, as discussed in what follows -- with its particular appeal to those deriving significance from archetypal symbols. Confrontation between contrasting languages itself offers a potential source of insight, recalling the value to surveying and mapping of a long baseline (Mathematical Theology: future science of confidence in belief, 2011). The latter was presented as a self-reflexive global reframing to enable faith-based governance.
It remains to be discovered whether emerging insights into wave theory will offer a meta-language which can be experienced as a generalization of such contrasting cognitive modalities -- each then to be understood as metaphors. The possibility has been tentatively suggested by Alexander Wendt (Quantum Mind and Social Science: unifying physical and social ontology, 2015), and discussed separately (Being a Waveform of Potential as an Experiential Choice: emergent dynamic qualities of identity and integrity, 2013; Wave-language potentially implied in encodings elaborated by cultures, 2013).
Stars and birds? Widespread use is made of stars on the flags of nations and intergovernmental institutions -- with little explanation of the associated symbolism and strategic implications, as discussed separately (Imagining the Flag of Europe otherwise? 2018). Given the importance of the flight metaphor in recognizing strategic achievement, such stars invite explanation in terms of the capacity of birds (Coordination of Wing Deployment and Folding in Politics, 2018). That framing developed the case for bird flight and landing as complementary metaphors of global strategic coherence under the following headings:
Winged angels and demons? A few passages of the Bible describe angels as stars (Revelation 9:1; 12:4; Job 38:7–8; Daniel 8:10; Judges 5:20). From a traditional perspective, it is somewhat extraordinary that "wings" should figure so frequently in the iconography of both demons and angels. For a secular society claiming to have transcended such framing, there is a case for exploring the transformation of the latter into problems and strategies respectively -- and in frequent reference to so-called political wings. In doing so, there is also a case for acknowledging the centuries of reflection on the manner of organization of the angelic and demonic realms -- especially given the continuing significance attributed to them by religious societies.
Extraordinary though it may appear from a secular perspective, it is noteworthy that King Charles III, in his message to the nation at his mother's passing made specific reference to angels (Alison Milbank "May flights of angels sing thee to thy rest": Elizabeth II and the virtues of a Christian monarchy, ABC Religion and Ethics, 13 Sep 2022). In the funeral itself, with its worldwide media coverage, reference was again made to angels and archangels, as in the commital service (Queen's funeral, The Sydney Morning Herald, 20 September 2022). Despite the attendance of world leaders, such language is not susceptible to challenge in practice (World leaders at Queen Elizabeth's funeral, Reuters, 20 September 2022). An exception has however been with regard to a much-cited speech by Vladimir Putin (Putin attacks West as 'satanic', hails Russian "traditional" values, Reuters, 30 September 2022).
From a secular philosophical perspective, it is intriguing to note that the "existence" in substantive terms of angels and demons is as tenuous and questionably founded as that of problems and strategies. More relevant is the effort invested in ordering such abstractions -- whether as artefacts of cultures or of collective awareness. There is also a case for respecting the engagement of the past with such matters -- whether readily deprecated with reference to scholastic debate regarding the "number of angels on the head of a pin".
It is appropriate to note the continuing interest in the acknowledged authority on angels, namely Thomas Aquinas -- still cited as Doctor Angelicus (Joseph M. Magee, Saint Thomas Aquinas and Angels, Aquinas Online; Gregory T. Doolan, Aquinas on the Demonstrability of Angels, A Companion to Angels and Medieval Philosophy, 2012; Thomas Aquinas, On the Angels, 2015. The Pontifical University of Saint Thomas Aquinas (PUST), also known as the Angelicum, is administered by the Dominican Order as the order's central locus of Thomist theology and philosophy.
The Second Vatican Council specifically encouraged continuing speculation on the nature of angels -- given their relationship to evangelization as the fundamental Christian mission (Gary Curtis, How Are Angels Involved in End-Times Evangelism? Charisma News, 18 May 2020; Pope John Paul II, Catechesis on the Angels, General Audiences, 1986).
Wicked problems and angelic strategies? It is of course the case that particular arrays of strategies, such as the 17 Sustainable Development Goals can be understood as having taken on the systemic role of distinct angels -- effectively held to embody what is deemed "sacred" in a secular society. They are arrayed against a set of problems -- effectively held to embody the wickedness by which the demonic has been traditionally recognized. Hence the current reference of the policy sciences to "wicked problems".
The manner in which they are widely suggests that values are are the "new sacred" for global civilization, especially democratic values, as discussed separately (Values, Virtues and Sins of a Viable Democratic Civilization, 2022). Similarly problems can be recognized as the "new demonic", appropriately confirmed by the extent to which "evil" continues frequently to be recognized and attributed to both phenomena and individuals (Existence of evil as authoritatively claimed to be an overriding strategic concern, 2016).
Any remedial contribution of the SDGs could of course be credibly described as "angelic" for public relations purposes, as noted by the United Nations with respect to the “Angel for Sustainable Development” Global Awards, as offered by the World Organization for Development (WOD). The awards celebrate winners in seven categories that correlate with 11 SDGs -- but not others? Award ceremonies will be held in cooperation with and under the auspices of UN bodies responsible for implementing the SDGs.
Memorable organization of the insubstantial? As discussed separately as an exercise in collective memory, there is therefore a case for exploring how the far vaster arrays of angels or demons (that are claimed to exist) might be organized in order to render them more memorable (Engaging with Hyperreality through Demonique and Angelique? 2016). This is partly justified by the extent to which the attributes of many individual angels or demons have been explicitly identified -- potentially to a higher degree than is deemed credible in the case of strategies and problems.
Noteworthy is the Angelicpedia list of 248 angels, and the related list of 111 fallen angels -- as with the Wikipedia List of angels in theology and the List of theological demons. Given their function roles from a systemic perspective, are these to be usefully compared with the arrays of strategies and problems in the Encyclopedia of World Problems and Human Potential?
The question here is then how such arrays might be comprehensibly organized, given that their number in each case has been claimed traditionally to be 72 -- namely far in excess of what is readily indicated as memorable in the case of problems or strategies. Whilst the number of angels and demons is variously held to be very extensive, there is the mnemonically enchanting possibility that the number held to be more comprehensible (and more memorably named) reflects a degree of intuitive recognition of the complex geometrical nexus of which the tetrahedral animation within the drilled truncated cube is indicative.
The relation between "angels" and "angles" is especially evocative in English, as an "angle of understanding", an "angle of insight", an "angle of perspective" -- or "having an angle"? There is a provocative case for recognizing angelology as the study of the geometry of coherence, of "heavenly" coherence -- hence sacred geometry --- with demonology as the study of the geometry of incoherence, of "hellish" incoherence. Problems could even be usefully recognized as "fallen values".
A similar comparison might be made with axiology as the study of "value space" -- with problemology as the study of "problem space", namely the world problematique (Alan Holland, The Value Space of Meaningful Relations, Human-Environment Relations, 2012; Sebastian Ostlund, Determining the Value-Space of Well-Being in the Capability Approach, Umea University, 2022; William R. Catton, Jr., A Theory of Value, American Sociological Review, 24, 1959, 3; Paris J Arnopoulos, Problemology: a definition of social problems, Concordia University, 1995; Alexander N. Christakis, Retrospective View of the Club of Rome Problematique, Institute for 21st Century Agoras).
Given the manipulative exploitation of propaganda, there is a tragic sense in which the challenge of misinformation can then be understood as the "demonic misappropriation of angelic perspectives". Advertising could be recognized as especially complicit in that process (Varieties of Fake News and Misrepresentation , 2019; Towards a Science of Misinformation and Deception, 2021). Given the ease with which evil is recognized in others, there is a curious irony to the extent to which one group's "angelic strategy" is readily perceived as onaother group's "demonic strategy" -- provocatively recalling polyhedral duality in which faces are transformed into points, and points into faces.
Response to the current global crisis has been provocatively framed as a battle between the "headless hearts" and the "heartless heads" (Challenge of the "headless hearts" to the "heartless heads"?, 2018). Potentially more provocative is the sense in which the former could be compared with an angelic perspective and demonic threats. The latter then invites comparison with a geometric preoccupation with angles, whether in terms of a fruitful perspective on problematic situations, or cunningly devising a devious angle of manipulative exploitation. For a secular society, the argument might even be considered more "realistic" than that of Matthew Fox and Rupert Sheldrake (The Physics of Angels: exploring the realm where science and spirit meet, 2014).
Spiritual entities with functions seemingly corresponding to angels are recognized in many religions -- and are similarly clustered. In Abrahamic traditions, for example, reference is variously (and extensively) made to:
- 4 archangels of the Talmud, "surrounding God's throne", and potentially corresponding to the sides or vertices of a tetrahedron
- 7 archangels, termed the angels "nearest to God", and potentially corresponding to the principal axes of a cube (Global ethical nexus of disparate challenges, 2022)
- 8 angels indicated in the Quran (Malaaikah), and potentially corresponding to the vertices of a cube, as with the 8 beatitudes of Christianity
- 10 ranks of angels of various schools of Judaism, and potentially corresponding to the 6 edges and 4 vertices of a tetrahedron
- 12 archangels, or 12 legions of angels, potentially corresponding to the edges of a cube (Chantel Lysette, Get to Know the 12 Archangels , BeliefNet, 2008)
The cognitive nexus, notably with respect to the Tetragammaton, continues to evoke a range of imaginative arguments of potential relevance (John A. Gowan, The Cosmic Tetrahedron, 27 Nov 2000; Symmetry Principles of the Unified Field Theory, arXiv:physics/9911060v4, 3 July 2009). Contrasting perspectives -- fundamental to conflicts between faiths -- can be recognized as contrasting ways of looking at a pattern whose dynamics may indeed take a seemingly cubic form.
Focus is naturally on the dimensions held to be "nearest to God" as this may be understood as framed by a cube -- together with its geometric transformations. Rather than any particular preference, the challenge may be how does geometry enable what is most coherently fundamental to be perceived as 3-fold, 4-fold, 5-fold, 6-fold, 7-fold, 8-fold, etc? Within the geometrical metaphor, insubstantial fundamentals may then be variously associated with vertices, edges, or sides, or what they frame -- in 3D or more. The 7-fold axial pattern is discussed separately with animations (Global ethical nexus of disparate challenges, 2022).
Do some belief systems focus on metaphorical "points" or "axes", where others focus on "sides"? (Reconciling Symbols of Islam, Judaism and Christianity, 2017).
| Selective indication of numbers associated with drilled truncated cube (excluding indication of 3-, 4-, and 5-valency vertices, as well as 3-, 4-, and 8-edged faces) |
|||||||
| 3-fold axes | 4 main sides | 5 face types | 6-faced cube | 7 principal axes | 8 corners | 9 edge types | 12-fold view |
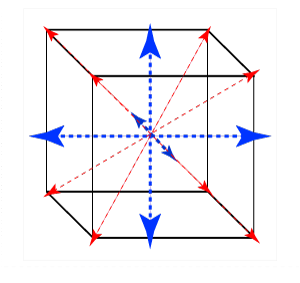 |
 |
 |
 |
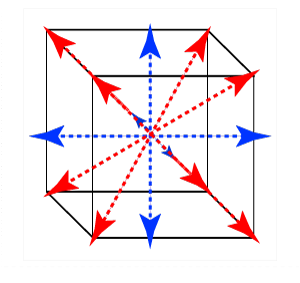 |
 |
 |
 |
| Elaborated with Stella Polyhedron Navigator | |||||||
If only for mnemonic purposes, the intuited sense of an "8-fold way" -- whether the Eightfold Path of Buddhism, of particle physics or of policy analysis -- can be usefully framed by the vertices or sides of a cube -- or of a stella octangula. The possible geometrical transformations of those forms are then especially indicative of related perspectives of which those forms are effectively resonance hybrids. The Chinese 8-fold pattern of BaGua trigrams is then particularly suggestive in the light of the much studied dynamic transformations between them. The tentative attribution of trigrams to the stella octangula (animations on right) is especially evocative of reflection in the light of its contrasting traditional configurations as framing dynamically a so-called "Earlier Heaven" and a "Later Heaven". For comparison, the corresponding traditional 4-fold attributions are made to the 4 sides of the tetrahedron (animation on left).
| Clues to comprehension of "housing" the insubstantial -- and the challenging dynamics of the container (animations exploding and imploding the simplest polyhedra forms) |
|||||
| Tetrahedron | Cube with octahedron | Octahedron with cube | Tetrahedron with tetrahedron | ||
 |
 |
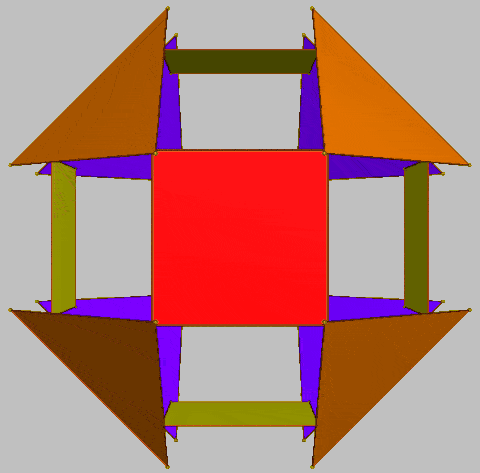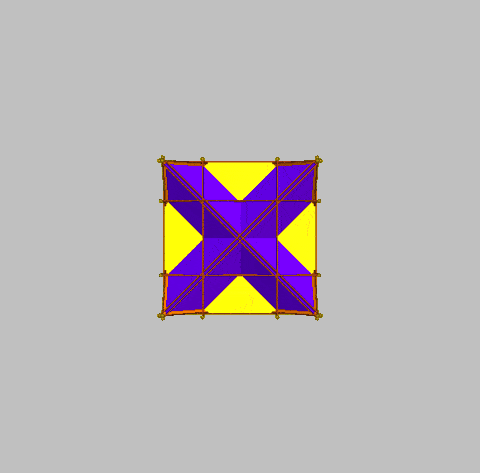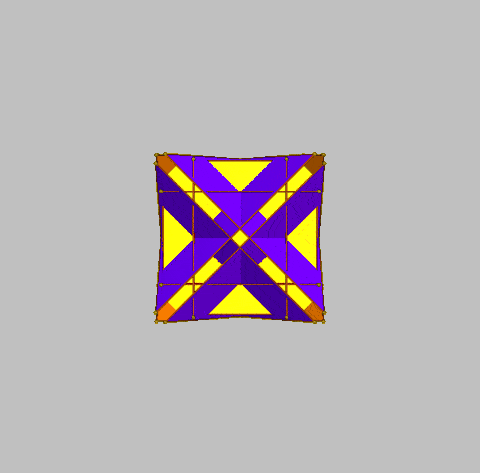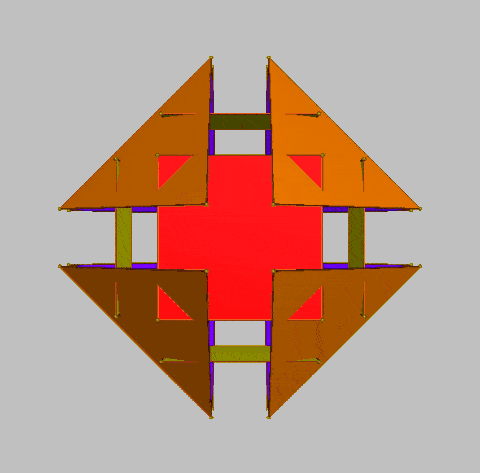 |
 |
 |
 |
| Animations made with Stella Polyhedron Navigator | |||||
Coherence may also be associated with types of vertices (valencies), sides (N-gonal), edges (lengths, parallels), or axes of symmetry. As with the much cited poem of Wallace Stevens (Thirteen Ways of Looking at a Blackbird, 1917), the challenge may be how many ways there are of looking at the "geometry" of the insubstantial -- beyond the pandemic discipline of the one right way (Interrelating Multiple Ways of Looking at a Crisis, 2021).
Following the polyhedral method used above, and in previous exercises, the pattern of 72 may be understood to factor as 8x9, 9x8, 6x12, or 12x6. The animation on the left below uses a 6-vertex octahedron to configure 6 icosahedra, each having 12 vertices. The central animations use an 8-vertex cube to configure 8 heptagrammic dipyramids, each having 9 vertices. That on the right uses a single heptagrammic dipyramid of 9 vertices to configure 9 8-vertex cubes.
| Exploratory polyhedral configuration of 72 elements | |||
| Octahedron configuring 6 icosahedra | Cube configuring 8 9-vertex heptagrammic dipyramids | Heptagrammic dipyramid configuring 9 cubes | |
 |
 |
 |
 |
| Animations made with Stella Polyhedron Navigator | |||
Traditionally intuited system diagrams for governance?
The set of modes of systemic negligence could well be recognized as "demons" for which vigilance is required in the governance of any system, as discussed separately (Evil loops and sigils as a pattern language, 2016). Any understanding of the relationship between sigil and demon therefore merits careful attention, whatever mapping device is used. A sigil could be recognized as a traditional systems diagram -- especially since "sigil is now used in computer programming. Demons then offer an imaginative means of distinguishing patterns of nonviability in systemic terms -- effectively of "unwholiness" or "unholiness". In geopolitical terms, an unholy alliance refers to an alliance perceived as unnatural, unusual, or simply undesirable, sometimes between seemingly antagonistic parties.
As a first exercise, on the assumption that the 72 traditional demons usefully characterize distinctive styles of problematic wickedness, experimental use can be made of a truncated icosahedron to configure the sigils deemed to represent them.
A much-cited traditional list of sigils is in The Lesser Key of Solomon. This presents the sigils of the 72 "princes of the hierarchy of hell" to be employed with the skills and understanding of traditional magic of the Ars Goetia. Within that worldview, such sigils have been considered to be the equivalent of the "true name of a spirit" and thus granted the magician a measure of control over them. Examples of such sigils include the following. Wikipedia offers a detailed List of demons in the Ars Goetia and a summary list of Goetic demons in popular culture (notably in role-playing games). The essence of a wicked problem, as a challenge to governance, could indeed be described metaphorically by such terms.
| Use of truncated icosahedron to display 2 sets of 32 demons linked by an octahedron displaying a set of 8 demons (thus totalling 72) |
||
| Version A mapping of 32 | Mapping of 8 | Version B mapping of 32 |
 |
 |
 |
| Generated using Stella Polyhedron Navigator | ||
The elements of the above animations are presented more clearly in the following animations which help to highlight the distinctive designs that can be used to populate the global configurations presented subsequently.
| Animation of sequence of 72 Angel names from the Shemhamphorasch (in two contrasting representations) |
Animation of sequence of 72 demonic sigils from the Ars Goetia (with matching reversed images) |
||
 |
 |
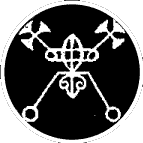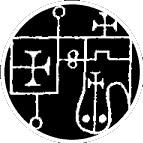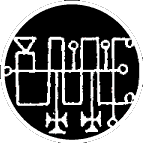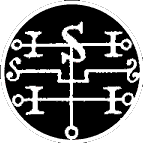 |
 |
Curiously it is however appropriate to note that there is currently no collection of systemically depicted problems which global governance is called upon to address. Ironically the nearest equivalent is the online Encyclopedia of World Problems and Human Potential from which what amount to specific systems diagrams are generated dynamically, as described and illustrated by Tomáš Fülöpp (Loop Mining in the Encyclopedia of World Problems, Paper for the 17th International Futures Conference on Futures Studies Tackling Wicked Problems, 2015).
The pathetic institutional response to the challenges of global governance is curiously echoed by the manner in which it is claimed to be founded upon "core democratic values" -- but with little ability to indicate what they are in any memorable systemic manner, as discussed separately (Core democratic values? 2022). It is for the defence of that ill-defined set of values that it is held necessary to engage in costly warfare, as in Vietnam, Afghanistan, and Ukraine, for example.
Interrelating "anglelique" and "demonique"? Configuring the global problematique as a whole has been limited to the world modelling exercises with which the Club of Rome report on Limits to Growth (1972) was originally associated. For example, the World3 model is a system dynamics model for computer simulation of interactions between population, industrial growth, food production and limits in the ecosystems of the earth (Alexander Christakis, A Retrospective Structural Inquiry of the Predicament of Mankind Prospectus of the Club of Rome, 2000). Little effort is made to depict the global problematique in memorable systemic terms -- especially in relation to any global resolutique of strategic responses (Patterning the Resolutique, Global Strategies Project).
There is therefore a case for considering how the "angelique" and the "demonique" might be configured -- in relation to one another, as discussed separately (Engaging with Hyperreality through Demonique and Angelique? 2016). This explores the mnemonic clues to global governance from mathematical theology and hyperbolic tessellation. It discusses Traditional modes of cognitive engagement with hyperreality and Hyperbolic reframing of the Demonique and Angelique of tradition. The following animations are reproduced from the latter discussion. The demonic metaphor can also be used to highlight the challenges to any remedial strategy (Mnemonic clues to 72 modes of viable system failure from a demonic pattern language, 2016).
| Indication in 2D of the dynamic nature of a "hyperdimensional" interaction between radically distinctive forces Alternative experimental configurations alternating between the 72 "angels" and 72 "demons" |
||
| Animation of 8 sets of 9 (enlargements for detail: angels / demons) |
Animation of 9 sets of 8 (enlargements for detail: angels / demons) |
The allocation of sets to the star "tables" in the schematics is based on the tabular form in which the 72 angel names (from the Shemhamphorasch) and the72 demonic sigils (from the Ars Goetia) are typically presented. See other presentations in the Wikipedia List of demons in the Ars Goetia (with comments on differences in variations between sources) and in The Demonic Paradise Wiki |
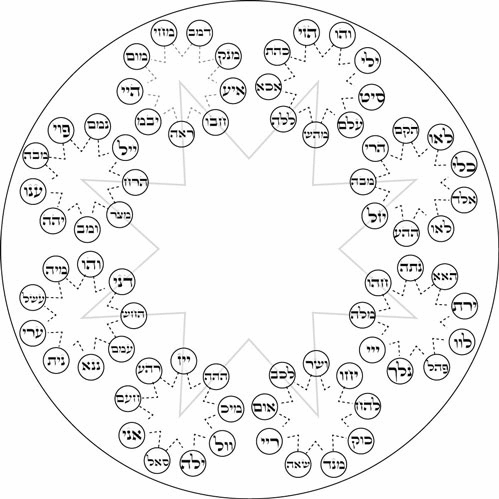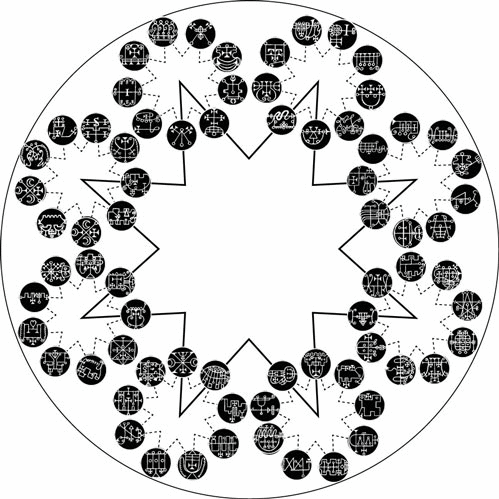 |
 |
|
| The rows are presented "around the tables" in one schematic, and the columns are presented "around the tables" in the other. The sequence around the tables is questionable, demanding further consideration from a systemic functional perspective. | ||
Implicit in any confrontation of 72 angels and demons is recognition of a capacity to make 144 distinctions (12x12) -- perhaps to be seen as a comparable challenge to memory to the 169 tasks (13x13) addressed by the 17 Sustainable Development Goals of the UN (Memorability of 17 Sustainable Development Goals with 169 tasks, 2020). Curiously there is one game which explores that degree of variety, namely mahjong with its use of 144 tiles, as discussed separately (Reframing the Righteousness Enabling Repetition of the Titanic Disaster: comprehension of 144 distinctions, 2020). Although from a culture with a distinctive iconography, this might then be seen as a game of "Angels" versus "Demons".
| Experimental mappings of angels and demons onto polyhedra | |||
| 72 Angels (as strategic values?) | 72 Demons (as "wicked problems"?) | ||
| Version A | Version B | Version A | Version B |
 |
 |
 |
 |
| Animations made with Stella Polyhedron Navigator | |||
Distinguishing requisite variety: requisite dependence on "other" perspectives
"Requisite variety"? Research on the control of complex systems by cybernetics makes a strong case for requisite variety. Biology makes a corresponding case with respect to genetic diversity in order to avoid the long-term vulnerability consequent on inbreeding. Despite such insights, the remarkable tendency is to favour a singular perspective, held to be challenged by any alternative perspective. This could be compared with any preference for a single gear in an automobile -- with the existence of other gears perceived as a direct challenge to its value.
This situation is only too evident in the governance of institutions, nations, and global civilization. Any "other" perspective is readily "demonised" and contrasted with a preferred approach held to embody uniquely the requisite values -- whether or not they are explicitly held to be "angelic". The preference is notably confused in any commitment to "evangelisation".
The difficulty, as highlighted in the development of this argument, is the human cognitive difficulty in eliciting coherence from diversity. Skills of any kind are typically dependent on modes of specialization which exclude the relevance of alternative perspectives. This is despite the recognized need for long baselines in surveying and mapping the environment, the globe and outer space -- most notably as an aid to navigation of the globe. For astronomy, this takes explicit form in very-long-baseline interferometry as implemented in the Very Long Baseline Array. In its focus on requisite consensus, governance tends to avoid such considerations and the justification for the forms it might necessarily have to take -- despite token multiculturalism.
Given the preference for singular frameworks in global governance, the preceding argument exemplifies the challenge in noting recognition of multiple perspectives -- whether in the articulation of values or strategies. "One Plan" thinking is inherently problematic -- however much its apparent coherence is appealing. Acknowledgement may be accorded to limited sets of values or strategic goals -- of which the 17 UN Sustainable Development Goals are an example.
At the same time, however, the challenges to effective governance are only too readily framed in terms of degrees of complexity which it is held to be unrealistic -- if not impossible -- to encompass. Everything is held to be problematically connected to everything. Ironically, institutionalisation of "oversight" responsibilities is then subtly characterized by "overlooking" and "blindspots". Paradoxically there is then an emergent need to depend on perspectives offered (even violently) by "others", although the integration of such multiplicity is far from the coherence enabled in the astronomical example. The "inexplicable" failures of interdisciplinarity and interfaith discourse make the point in practice.
Comprehension of the "requisite variety of otherness"? It could then be asked how many distinct perspectives are required for appropriate governance. How many contrasting methodologies are to be valued? There is little sense of how to evaluate the relevance of the extensive range of disciplines, especially given the tendency of their proponents and practitioners to selectively frame each other as irrelevant, as can be variously argued (Encyclopedia of Conceptual Insights from the World's Cultures, 1988; Enhancing the Quality of Knowing through Integration of East-West metaphors, 2000; Intellectual Disciplines and Sciences: cross-referenced to world problems, 1976).
As argued above, beyond the question of "how many" there is the challenge of comprehension of the distinctive modalities identified or claiming relevance of their particular perspective. The challenge is exemplified by the archetypal roundtable in which the qualities and attributes of one or the other may be separately recognized, but not that of all 12. As noted, the nature of the discourse between all 12 Apostles assembled at the Last Supper has evoked little interest -- as with that between the 12 Imams of Islam. By contrast, much is made of the identification of particular apostles as saints -- with the discourse that that evokes. If 12 key disciplinary modalities were to be recognized, how would the communication between them be framed? In systemic terms, the question is of course of relevance to the 17 SDGs of the United Nations -- with each variously acclaimed as an absolute priority.
The challenge of coherence can be exaggerated to the point of absurdity with respect to comprehension of the highest order of symmetry as yet discovered -- termed the Monster Group by mathematicians exploring it through "moonshine theory". As an exceptional form of symmetry, this could be recognized as a problematic Rosetta stone for cognitive frameworks (Potential Psychosocial Significance of Monstrous Moonshine, 2007; Dynamics of Symmetry Group Theorizing: comprehension of psycho-social implication, 2008). These commentaries note the paradoxical disinterest in comprehension of those preoccupied with the geometry of symmetry.
More simply, the question for governance can then be framed in terms of the human capacity to distinguish appreciatively between 2-fold, 12-fold, 64-fold, 72-fold, and N-fold perspectives, for example. Given the challenge, and the constraints on human memory, how is the requisite capacity to be effectively "outsourced" to others -- those preferring one modality rather than another?
Whilst this process is evident in that of specialization, the further challenge lies in the dramatic erosion in the quality of discourse between the "others" variously charged by society with "remembering" (Symbolizing Collective Remembering Otherwise, 2018; Reintegration of a Remaindered World: cognitive recycling of objects of systemic neglect, 2011; Societal Learning and the Erosion of Collective Memory, 1980). The challenge was notably described by Nicholas de Cusa (De docta ignorantia, 1440).
Distinguishing higher orders of process coherence? The software through which the forms above were generated invites exploration of the possibility of increasing the length of the polyhedron edges. As shown in the first image below left, a proportion of the edges converge to intersect with one another, thereby framing the drilled truncated cube in a manner which evokes new interpretations of a potentially higher order of coherence.
| Tetrahedral compound generated by experimental extension of selected edges of the drilled truncated cube | ||
| Indication of extension of selected edges | Correspondence to 8-pointed star (6-fold) | |
 |
 |
 |
| Interactive 3D variant | ||
That polyhedron is presented within the animation above left, the second being a wire frame rendering rendering its faces transparent. Inspection of the image, and its interactive 3D variant, usefully frames the question of the number of interlocking structures that can be distinguished -- and by whom. It is in fact a compound of 8 interlocking tetrahedra. However, in terms of the psychosocial functions it might be used to contrast, can this be readily and unambiguously distinguished from a compound of 6 interlocking tetrahedra, or one of fewer or greater interlocking tetrahedra? The variety of these compounds, as polyhedra in their own right, has been the subject of particular geometrical commentary (George Hart, Harman's Compounds, 1996; Marcel Tünnissen, Compounds of Tetrahedra, 2007; Compounds of Tetrahedra for Platonic Symmetries, 2022).
The relative complexity of these tetrahedral compounds offers valuable insights with respect to the corresponding challenge of distinguishing between psychosocial functions of increasing subtlety -- if it is assumed that these might be fruitfully associated with such configurations, and distinctively clustered as subsystems. The concern relates to comprehension in terms of geometry of the arguments of oppositional logic, as noted above. The contrasts between the following help to focus questions relating to confusion, conflation and incomprehension ("ignorance") with regard to subtle distinctions and their role in relation to coherence of ever higher order.
| Compounds of tetrahedra as indications of challenges to comprehension of coherence (with wire frame renderings and properties with which conceptual insights might be associated) |
||||
| 2 tetrahedra | 3 tetrahedra | 4 tetrahedra | 6 tetrahedra | 8 tetrahedra |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 8V, 12E, 8F (16VF) | 12V, 18E, 12F (24VF) | 16V, 24E, 16F (32VF) | 24V, 36E, 24F (48VF) | 32V, 48E, 32F (64VF) |
| Animations prepared using Stella Polyhedron Navigator | ||||
There is a case for using the geometrical distinctions above to recognize the relative ease (or difficulty) of comprehension of the subtle distinctions intuited in the traditional belief systems in which so much reflection has been invested over centuries. For example, in the light of the number of features of these polyhedra (on which insights may be variously "hung" for mnemonic purposes):
- 2-tetrahedra complex (or stella octangula): indicative of the coherence associated with 8-fold and 12-fold patterns most readily comprehended
- 3-tetrahedra complex: offers a new context for 12-fold coherence, and offers a frame for the 18-fold sets valued in Judaism, Hinduism and Babism.
- 4-tetrahedra complex: offers a context for the 16 possible binary Boolean operations, which are a focus for the geometrical representation of oppositional logic and the associated truth tables distinguishing true and false (although use is typically made of polyhedra with 14 vertices, by declaring 2 of the 16 distinctions to be unnecessary). Given the consideration above of the UN SDGs as a 16-fold pattern, it is of some relevance whether a 4-tetrahedral clustering would offer a more coherent and comprehensible approach to the set as a whole, in contrast to other approaches (Salil K. Sen and Viput Ongsakul, Clusters of Sustainable Development Goals: a metric for grassroots implementation, Sustainability, 11, 2018, 3)
Intriguingly (as discussed below) the complex offers a bridging context to 24-fold patterns proposed or intuited in contexts alien to conventional logic. An effort has been made separately to visualize the possible interplay between 24 distinct voices in the light of the construction of the 4-fold lauburu symbol of Basque culture (24-fold Pattern Implied by Dynamics of the Lauburu in 3D, 2016; see interactive variant).
- 6-tetrahedra complex:
- 24-fold organization: With respect to the nature of the coherence with which this pattern might be associated, the Wikipedia profile on the number 24 provides a surprisingly extensive list. This notably includes:
- The tesseract (to which reference was made above) has 24 two-dimensional faces (which are all squares). Its dual four-dimensional polytope is the 16-cell, which has 24 edges.
- 24 is the kissing number in 4-dimensional space: the maximum number of unit spheres that can all touch another unit sphere without overlapping. (The centers of 24 such spheres form the vertices of a 24-cell).
Curiously unquestioned, 24 is the number of hours in a day (rendering its experience widely familiar as a means of organizing time) -- and most obviously as the total of 24 major and minor keys in Western tonal music. Following the discussion of the previous section, 24 features variously in different religions: the number of books in the Tanakh of Judaism; the number of spokes in the Ashok Chakra of Hinduism; and the number of Tirthankaras in Jainism. In Christian apocalyptic literature it represents the complete Church, being the sum of the 12 tribes of Israel and the 12 Apostles of the Lamb of God. For example, in Revelation 4:4: Surrounding the throne were twenty-four other thrones, and seated on them were twenty-four elders. They were dressed in white and had crowns of gold on their heads. Nevertheless, as argued with respect to the 12 participants in any archetypal roundtable, little has been said regarding the interaction between such disparate voices.
- 24-fold organization: With respect to the nature of the coherence with which this pattern might be associated, the Wikipedia profile on the number 24 provides a surprisingly extensive list. This notably includes:
- 36-fold organization: Again particular significance has been attached to a 36-fold pattern by religions in distinguishing the Absolute, whether in the case of Judaism, Shavism, or that of Ancient Egypt. Potentially of particularly comprehensible value in distinguishing the articulated insights are the Thirty-Six Stratagems of Chinese tradition, deemed appropriate as approaches to conflict situations. Similar consideration is merited with respect to The Thirty-Six Dramatic Situations of theatre, given the insights they may offer to governance as a a dramatic form in its own right (Thirty-six Dramatic Situations faced by Global Governance? 2022).
- 8-tetrahedra complex:
- 32-fold organization: This pattern has been variously discussed in the argument above. Again the Wikipedia entry notes recognition of the 32-fold pattern in various religions, including Buddhism, Hinduism and Judaism.
- 48-fold organization: In striking contrast to the variety of 24-fold patterns, the 48-fold appears to have been primarily recognized through:
- the highly disciplined practice of Nianfo of Pure Land of Buddhism (Cheng Wei-an, Taming the Monkey Mind: a guide to Pure Land Practice, Buddha Dharma Education Association, 2000; Charles B Jones, Chinese Pure Land Buddhism: understanding a tradition of practice, 2020)
- the classic collection of 48 Zen koan, compiled in 1228 by the Chinese Zen master Wumen Hui-k'ai, is known in Mandarin as Wúménguan and in Japanese as Mumonkan. Consistent with its paradoxical subtlety, it is commonly translated in English as The Gateless Gate, although the implications of this are contested -- as evident in the translation by Robert Aitken (The Gateless Barrier, 1991). Experimentally the set has been adapted for Twitter, with the tweets configured on polyhedra (Configuring a Set of Zen Koan as a Wisdom Container, 2012).
These contrasts help to clarify the extent to which the subtler distinctions, deemed appropriate to a sense of fundamental coherence, are increasingly elusive as an ever-increasing "cognitive stretch" -- and are then readily dismissed as a consequence. The 64-fold pattern of the I Ching -- with which the 8-tetrahedra complex has been shown to be associated -- therefore merits consideration as a bridging pattern. This is especially the case given its traditional value to civil governance and the manner in which it addresses the challenge of the comprehensibility of its highly articulated elusive distinctions through metaphor.
Given the challenge of reconciling the "heartless heads" and the "headless hearts", it is suggestive to see these modalities reflected in that between the abacus and circlets of prayer beads (Designing Cultural Rosaries and Meaning Malas to Sustain Associations within the Pattern that Connects, 2000). Beyond the constraints of both metaphors, movement along interweaving circuits within a polyhedral form potentially offers a means of rendering explicit coherence of a higher degree (Spherical Accounting: using geometry to embody developmental integrity, 2004).
Variable geometry of institutions as alternation between comprehensible polyhedral patterns
There is continuing reflection on the possibility of a "variable geometry" of regional and institutional organization:
- Susan George: Variable Geometry to Design Positive Outcomes (Transnational Institute, 2005)
- Rosalyn Higgins: The Concept of 'The State': variable geometry and dualist perceptions, 2009).
- Elisa Tino: The Variable Geometry in the Experience of Regional Organizations in Developing Countries (Spanish Yearbook of International Law, 2013)
- James Thuo Gathii: Variable Geometry: a defining aspect of African RTAs (African Regional Trade Agreements as Legal Regimes, 2011)
- Matthew P. Goodman: Variable Geometry Takes Shape in Biden's Foreign Policy (Center for Strategic and International Studies, 19 March 2021)
The possibility has been most developed with respect to a multi-speed Europe:
- Patrick Joachim Dunphy: Variable Geometry Europe: patching together what works in the fight against hard-core cartels: carrots, sticks, custody and leniency (Institute for Trade and Commercial Law, February 2007)
- Charles Grant: Can Variable Geometry Save European Enlargement (CER Bulletin, October/November 2005, 44)
- J. A. Usher: Variable Geometry or Concentric Circles: patterns for the European Union (International and Comparative Law Quarterly, 46, 1997)
- Peter Van Elsuwege: Variable Geometry in the European Neighbourhood Policy: the principle of differentiation and its consequences
The relevance has been explored with respect to the United Nations (Alternation between Variable Geometries: a brokership style for the United Nations as a guarantee of its requisite variety, 1985).
The reference to transmission systems for gear-changing (as discussed above) can clearly be recognized as an application of the potential of variable geometry. The questions is how this can be related to the transformation between polyhedral patterns exemplifying alternation between contrasting patterns of movement of information.
The potential of variable geometry could well be especially relevant to the challenging relationships between divided countries (Korea, Israel-Palestine, China-Taiwan, and the like). With the passing of Elizabeth II, the possibility merits consideration with respect to the future role of monarchy, most notably in relation to the future organization of the Commonwealth of Nations. More controversially is its relevance to the organization of NATO (Alastair Crooke, A Variable Geometry NATO? Really? Al Mayadeen 29 May 2022). As argued separately, the potentially hidden faces of global strategy might well be highlighted through polyhedra (Envisaging NATO Otherwise -- in 3D and 4D? 2017).
References
Keith Albar. The Language of Pattern: an enquiry inspired by Islamic decoration. Thames and Hudson, 1974
Aquinas, Thomas:
- On the Angels. CreateSpace Independent Publishing, 2015
- Treatise On The Angels. Summa Theologiae, QQ 50-64 [contents]
Stafford Beer. Beyond Dispute: the invention of team syntegrity. John Wiley, 1995
David Bohm. Wholeness and the Implicate Order. Routledge and Kegan Pual, 1980
Keith Critchlow:
- Order in Space: a design source book. Thames and Hudson, 1969
- Islamic Patterns: an analytical and cosmological approach. Thames and Hudson, 1976
- The Hidden Geometry of Flowers: living rhythms form and number. Floris Books, 2011
Marcus du Sautoy:
- Symmetry: a journey into the patterns of nature. HarperCollins, 2008 [review]
- Finding Moonshine: a mathematician's journey through symmetry. Fourth Estate, 2007 [review] [review]
- The Music of the Primes. Fourth Estate, 2003 [review]
Matthew Fox and Rupert Sheldrake. The Physics of Angels: exploring the realm where science and spirit meet. Monkfish Publishing, 2014 [summary]
R. Buckminster Fuller with E. J. Applewhite:
- Synergetics: explorations in the geometry of thinking. Macmillan, 1975 [text]
- Synergetics 2: further explorations in the geometry of thinking. Macmillan, 1979 [text]
Susan George. Variable Geometry to Design Positive Outcomes. Transnational Institute, 2005 [text]
Charles Grant:
- Variable Geometry. Prospect Magazine, July 2005 [text]
- Can Variable Geometry Save European Enlargement. CER Bulletin, October/November 2005, Issue 44 [text]
Louis H Kauffman, Jytte Brender Mcnair, Lynnclaire Dennis. The Mereon Matrix: everything connected through (k)nothing. World Scientific, 2018
Alfred Koryzbski, Science and Sanity: an introduction to Non-Aristotelian Systems and General Semantics. Institute of General Semantics, 1994
Jeremy Lent. The Patterning Instinct: a cultural history of humanity's search for meaning. Prometheus, 2017 [contents]
Ernest McClain:
- Myth of Invariance: the origins of the gods, mathematics and music from the Rg Veda to Plato. Nicolas-Hays, 1976
- The Pythagorean Plato: prelude to the song itself. Nicolas-Hays, 1978
- Meditations Through the Quran: tonal images in an oral culture. Nicolas-Hays, 1981
Ann E. Moyer. The Philosophers' Game: rithmomachia in Medieval and Renaissance Europe. University of Michigan Press, 2001
Anthony Pugh. Polyhedra; a visual approach. University of California Press, 1976.
Robert D. Romanyshyn. Technology as Symptom and Dream. Routledge, 1989
Alexander Wendt. Quantum Mind and Social Science: unifying physical and social ontology. Cambridge University Press, 2015
Robert Williams. Natural Structures: toward a form language. Eudaemon Press, 1972
Frances Yates:
- The Art of Memory. Routledge and Kegan Paul, 1966
- Giordano Bruno and the Hermetic Tradition. University of Chicago Press, 1964
|
For further updates on this site, subscribe here |


